GMAT Question of the Day – Data Sufficiency – Geometry

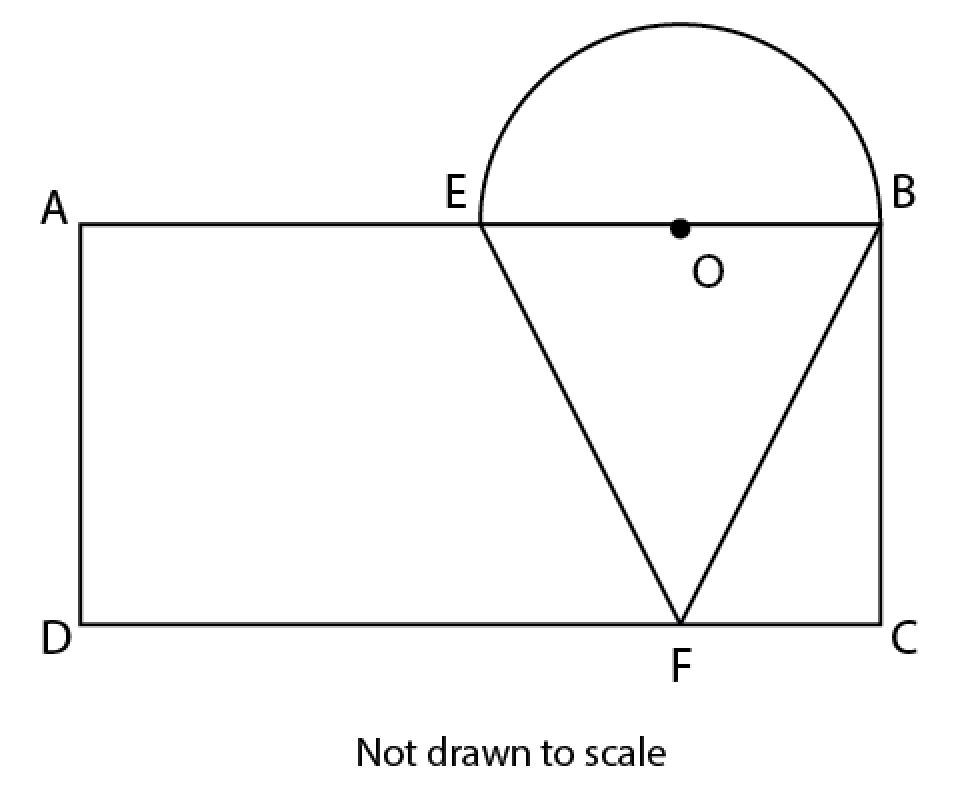
In the diagram above ABCD is a rectangle. EB is a semi-circle with center O and a radius of 2.  What is the area of triangle CBF?

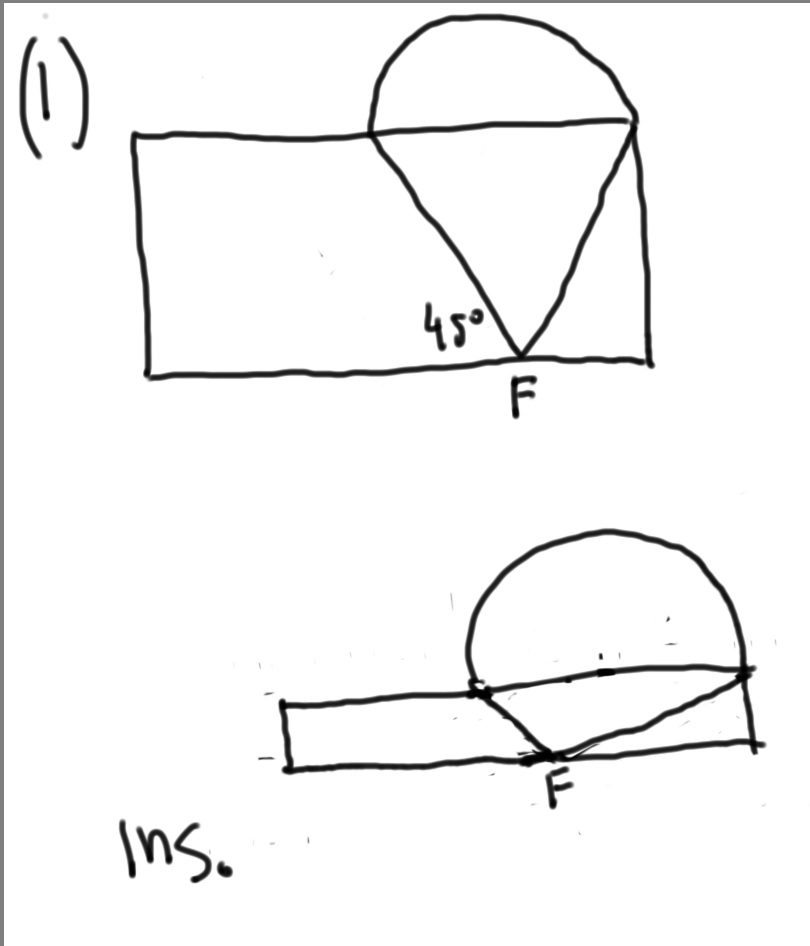
(1)  Angle EFD = 45 degrees

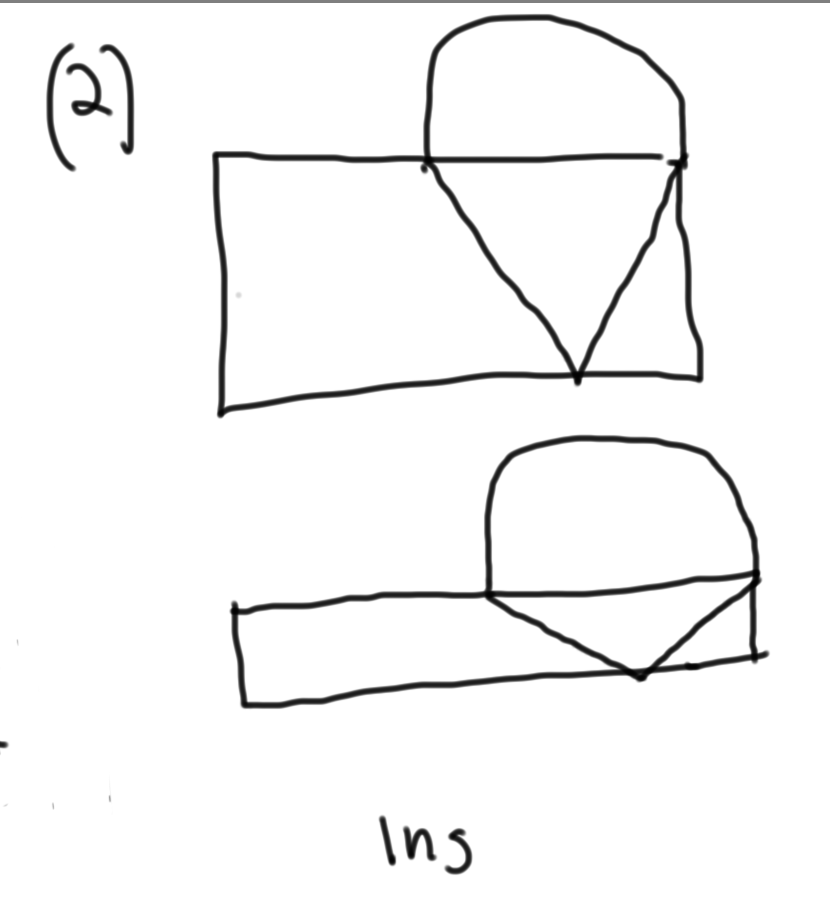
(2)  Angle BEF = Angle FBE

GMAT Question of the Day Solution (if you just want the answer scroll to the bottom!)

How do you prove insufficiency in a GMAT geometry question? Either show that two values are possible for the answer or (and this is basically the same idea) show that the shape can be distorted to produce many different values. Sometimes it’s tough to show different values because you can’t necessarily calculate the different scenarios. In these cases it’s easier to show that the shape can be distorted.

(1) You can see in the diagrams that if the height of the rectangle changes we can still maintain the 45 degree angle by shifting point F to left and consequently change the area of triangle CBF. Insufficient.

(2) This means that triangle EBF is isosceles but still the angles can vary so the area of triangle CBF can also vary. Insufficient.

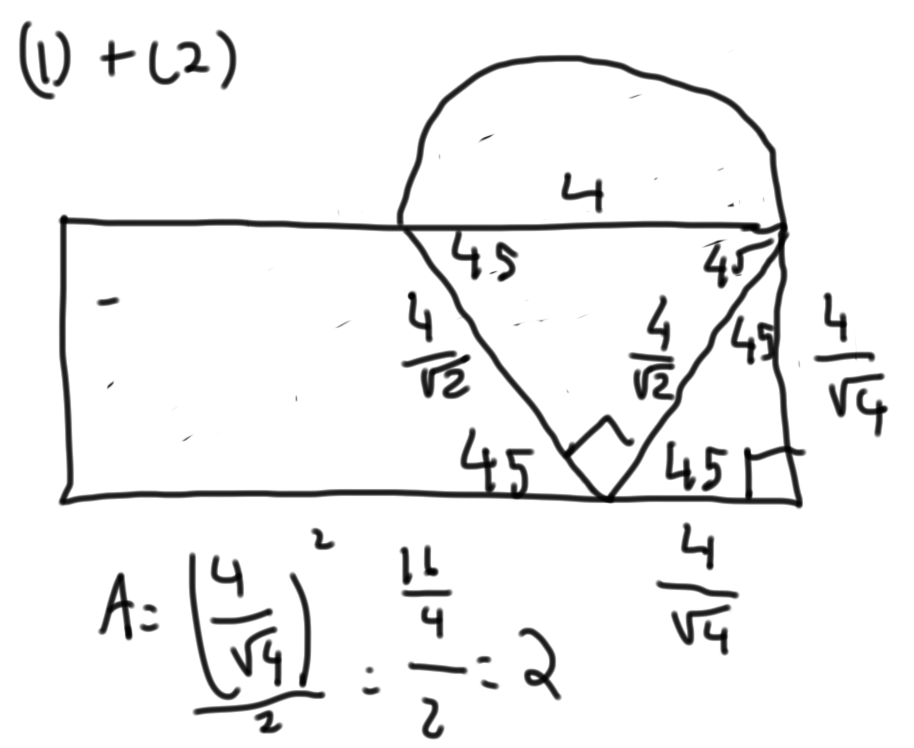
(1) + (2) If you put the statements together you know that EBF is a right isosceles and that CBF is also a right isosceles. The sides are in a ratio of 1:1:root 2. With this information you can calculate all of the sides and have a definite value for the area of triangle CBF.  Sufficient.

[spoiler]C.[/spoiler]

Sign up for 1 challenging GMAT question and solution per week

If you’d like a challenging GMAT question sent to you once a week go ahead and sign up with the form below. We have hundreds of great questions that for this email list we’re narrowing down to the best of the best. We won’t send you anything else. Unsubscribe whenever you want.

Additional GMAT Data Sufficiency Yes/No Distortion Practice Questions

Here’s an Official GMAT Question that has different Geometry content but uses the same distortion and yes/no strategy: GMAT Official Guide Geometry Yes/No Example

Here’s a Geometry Yes/No question from the GMAT Question of the Day.

And another challenging Geometry GMAT Question of the Day

Last but not least a very tough Yes/No coordinate plane question from the GMAT Official Guide: In the xy-plane, region R consists of all the points (x,y) such that 2x + 3y ≤ 6. Is the point (r,s) in region R?

How to work with us

All of the intake info we need to schedule an initial call to see if we are a good fit.