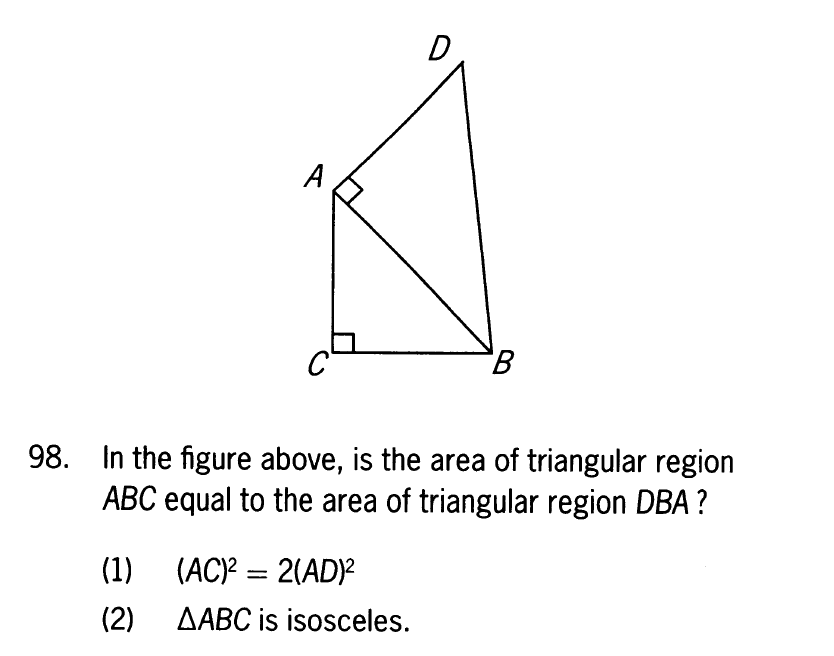
In the figure above, is the area of triangular region ABC

In the figure above, is the area of triangular region ABC equal to the area of triangular region DBA? GMAT Explanation

in the figure above, is the area of triangular region abc equal to the area of triangular region dba? diagram

In the figure above, is the area of triangular region ABC equal to the area of triangular region DBA?

(1) (AC)^2 = 2(AD)^2

(2) ∆ABC is isosceles.

This is a tough GMAT Data Sufficiency question from the Official Guide. We’ll be attacking it with Yes/No and distortion. But first let’s make sure to read carefully and define the question. Get a sense for the diagram and make some inferences. We want to know whether the area of triangular region ABC is equal to the area of triangular region DBA. We have two right triangles so let’s keep in mind that right triangles have certain properties and could be special right triangles, 45-45-90 (right isosceles) or 30-60-90 or some special ratio 3-4-5, 5-12-13.

Not much to do with the diagram so let’s jump into statement (1) (AC)^2 = 2(AD)^2

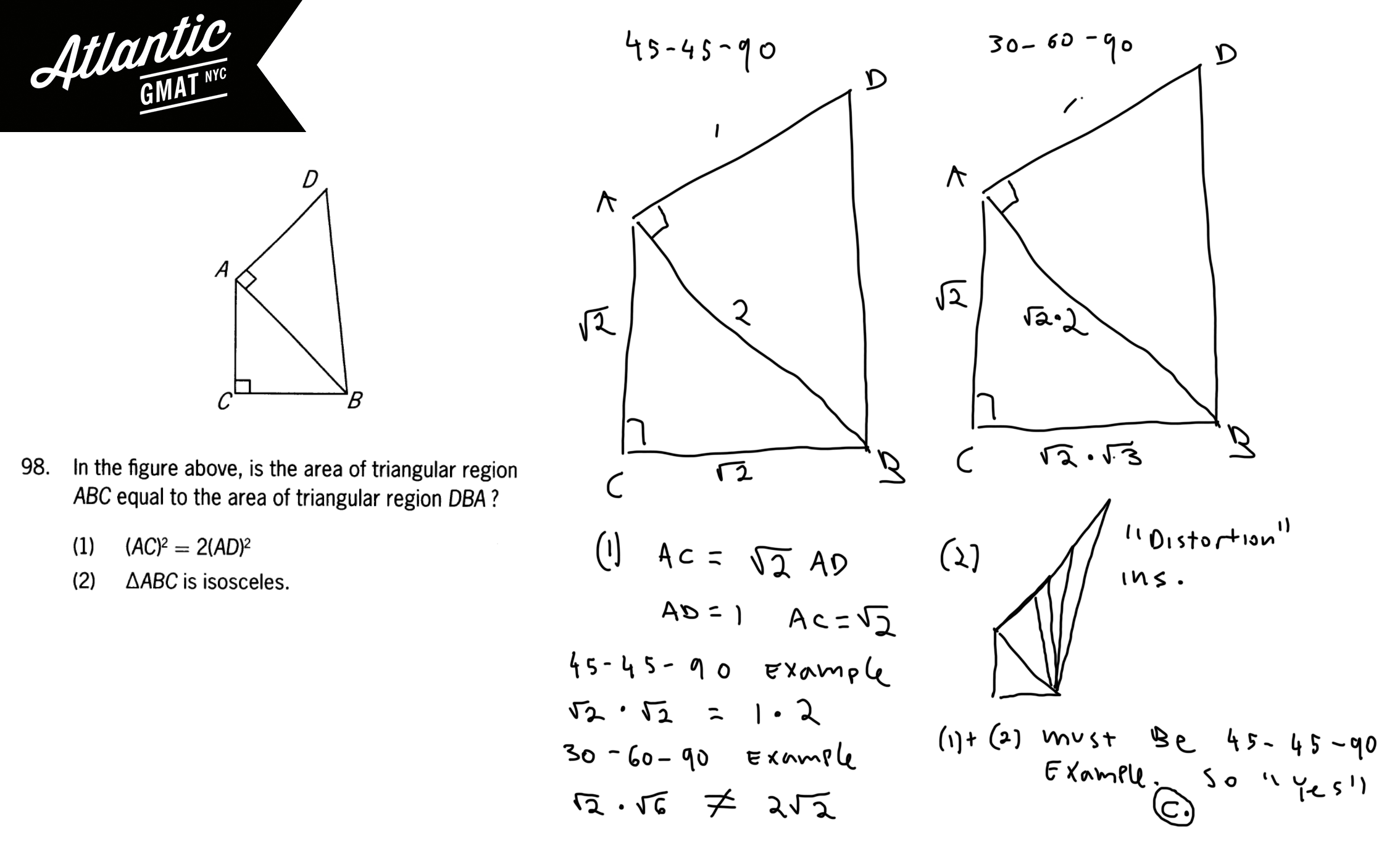
We can pick some values that follow that ratio. Let’s make AD = 1 so AC must be √2. Now let’s go ahead and do a Yes/No. You might think, hmmm, there are a million value I could pick. This is getting confusing… That’s true. However, let’s keep it easy. Especially because you know that you have two right triangles. Use special triangles as the side ratios will be defined for you. Also, GMAT loves special triangles so they are often a great bet for scenarios on GMAT DS. So let’s try a 45-45-90 configuration and see where that takes us and then a 30-60-90 and see if that agrees or not.

If AC = √2 then CB also equals √2 leaving the area for triangular region ABC at 1. Because of 45-45-90 (or Pythagorean theorem) AB equals 2. So, with AD = 1 and AB = 2 the area of triangular region DBA is also 1. So in this case the area of triangular region ABC  is equal to the area of triangular region DBA. That gives us a clear “Yes”. But that’s only one scenario. For GMAT DS we have to try to prove insufficiency. Now let’s see what happens with a 30-60-90.

AC = √2 CB = √6 so the area is √12/2

AD = 1 AB = 2√2 (because of 30-60-90 rules) so the area is 2.

With a 30-60-90 example the area of triangular region ABC  is not equal to the area of triangular region DBA. Because we proved a “yes” and a “no” statement 1 is insufficient.

Let’s take a look at statement (2)∆ABC is isosceles.

For this one we can use “distortion”. Keep triangular region ABC the same but see if you can change the size of triangular region DBA. You’ll notice that you can grossly distort DBA clearly changing the area. Because you can change the area of DBA while leaving ABC unchanged statement (2) is insufficient.

Now let’s put the statements together. Statement (2) constrains us to 45-45-90 and statement (1) tells us that if the triangular region ABC is a 45-45-90 then the area of triangular region ABC is equal to the area of triangular region DBA. We have a clear “yes” and there are no other possibilities so together the statements are sufficient. The answer is C.

in the figure above, is the area of triangular region abc equal to the area of triangular region dba? full solution diagram

There are two GMAT Data Sufficiency strategies we worked on here:

  1. Yes/No. With a question that asks for a yes or no answer organize your solution into Yes/No. Write Yes and No on your paper to remind yourself that you need to try create scenarios that prove a yes and a no.
  2. Distortion. This can be very helpful for getting through tough geometry questions very quickly. Try to manipulate the shape while respecting whatever constraints there are in place. If you can shift the size of one shape vs another or one angle vs another you can easily prove insufficiency without doing any calculations.

Additional GMAT Data Sufficiency Yes/No, Distortion, Geometry Practice Questions

Here are a bunch of DS Yes/No examples. A couple are very similar a couple are somewhat different but for all of them you can used either Yes/No or Distortion. I’d work through all of these to master those concepts.

Here is another challenging geometry question with right isosceles triangles: The perimeter of a certain isosceles right triangle is 16 + 16√2. What is the length of the hypotenuse of the triangle?

Here’s a very similar Geometry Yes/No Distortion question from GMAT Question fo the Day

Here’s another GMAT Question of the Day Geometry Distortion example.

And one more GMAT Question of the Day Yes/No example.

Here’s an Official GMAT question with Yes/No strategy: In the xy-plane, region R consists of all the points 

This GMAT Question of the Day Geometry example isn’t really a Yes/No question because you are looking for a specific value but you can still use Yes/No and Distortion to prove insufficiency

Also, Yes/No isn’t just for Geometry. Here’s a Yes/No divisibility example from the GMAT Official Guide