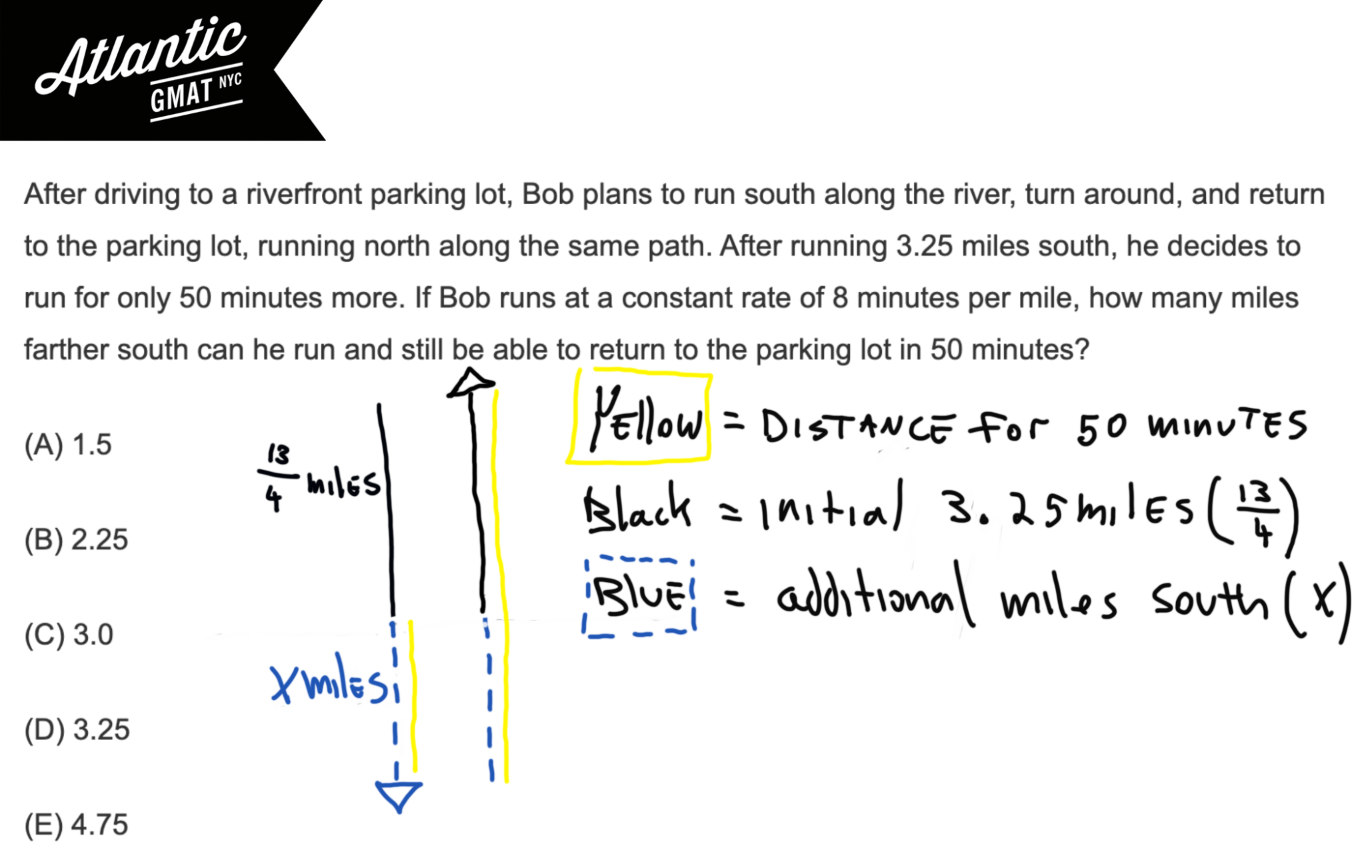
After driving to a riverfront parking lot, Bob plans to run south along the river, turn around, and return to the parking lot, running north along the same path. After running 3.25 miles south, he decides to run for only 50 minutes more. If Bob runs at a constant rate of 8 minutes per mile, how many miles farther south can he run and still be able to return to the parking lot in 50 minutes? GMAT Explanation, Video Solution, and More Practice Questions!

After driving to a riverfront parking lot, Bob plans to run south along the river, turn around, and return to the parking lot, running north along the same path. After running 3.25 miles south, he decides to run for only 50 minutes more. If Bob runs at a constant rate of 8 minutes per mile, how many miles farther south can he run and still be able to return to the parking lot in 50 minutes?

(A) 1.5

(B) 2.25

(C) 3.0

(D) 3.25

(E) 4.75

Here’s another work and rate example from the GMAT Official Guide. This one has very little follow through but can be challenging to set up. We see this one a lot in tutoring sessions. The mistake we see over and over again on this question and many others: rushing the reading and setup in favor of execution. There are a ton of GMAT questions that are mostly setup with very little execution (this one for instance). Setup will always help!

Ok, let’s go ahead and define the question: how many miles farther south can he run and still be able to return to the parking lot in 50 minutes?

So we want to figure the extra part of the run. We’ve got the initial journey (13/4 miles) then the extra (which we’re solving for so let’s call it “x”) and then the return trip which is x + 13/4 (3.25 miles). To the extent that you can make the thing you’re solving for the variable. Diagram below to make this clear.

after driving to a riverfront parking lot, bob plans to run south along the river gmat explanation diagram

 

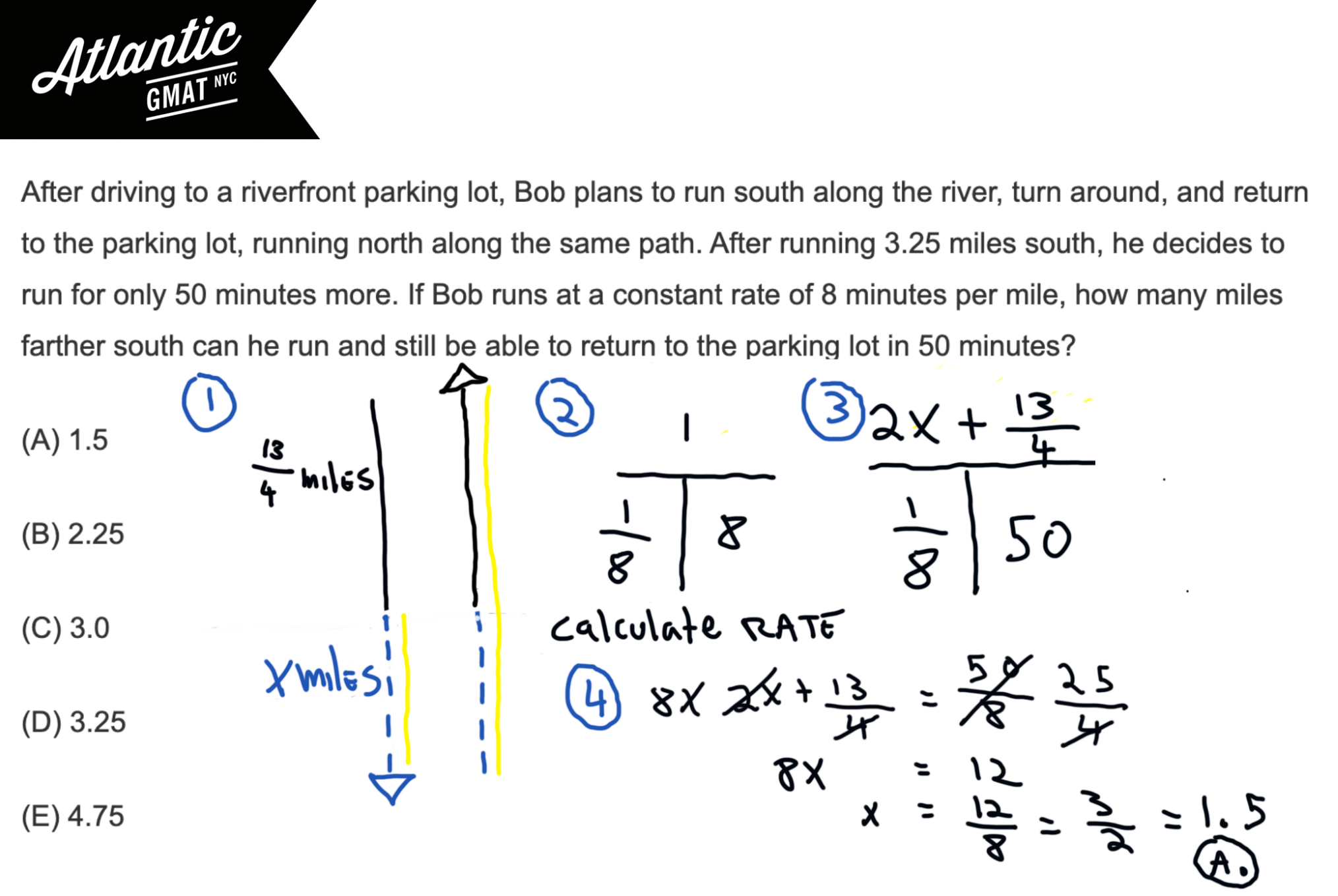
Now we need to solve for the number of miles he can run while still getting back in 50 minutes. So set the time at 50 minutes. Set the rate at 1/8 (a constant rate of 8 minutes per mile). The distance is the trickiest part but once you’ve got the diagram shouldn’t be a problem. It’s the extra distance x, plus the extra distance back x, plus the original distance 13/4 (3.25 miles). So 2x + 13/4. That’s it. Pop that information into a rate T, solve for x, and you’re done!

50/8 = 2x + 13/4

50 = 16x + 26

16x = 24

x = 24/16

x = 1.5

How many miles farther south can he run and still be able to return to the parking lot in 50 minutes? 1.5 A.

Here’s the entire solution in a diagram:

after driving to a riverfront parking lot, bob plans to run south along the river gmat explanation complete daigram

Video Solution: After driving to a riverfront parking lot, Bob plans to run south along the river, turn around, and return to the parking lot, running north along the same path. After running 3.25 miles south, he decides to run for only 50 minutes more. If Bob runs at a constant rate of 8 minutes per mile, how many miles farther south can he run and still be able to return to the parking lot in 50 minutes?

Additional GMAT Work and Rate Practice Questions

Here are another pair of challenging work and rate questions from the GMAT Official Guide on which you can practice setup at rate T’s:

During a trip, Francine traveled x percent of the total distance

Working simultaneously at their respective constant

And here is a very challenging work and rate question from the GMAT Prep Official Practice Tests

And a very typical but challenging cooperative rate question from the GMAT Prep Tests:

Mary passed a certain gas station on a highway while traveling west at a constant speed of 50 miles per hour. Then, 15 minutes later, Paul passed the same gas station while traveling west at a constant speed of 60 miles per hour. If both drivers maintained their speeds and both remained on the highway for at least 2 hours, how long after he passed the gas station did Paul catch up with Mary?

And another three questions from GMAT Question of the day:

GMAT Question of the Day Distance, Work and Rate – Average Rate 1

GMAT Question of the Day Distance, Work and Rate – Average Rate 2

GMAT Question of the Day Distance, Work and Rate – Average Rate 3