Working simultaneously at their respective constant rates, Machines A and B produce 800 nails in x hours. Working alone at its constant rate, Machine A produces 800 nails in y hours. In terms of x and y, how many hours does it take Machine B, working alone at its constant rate, to produce 800 nails? GMAT Explanation, Video Solution, and Additional Practice Questions.
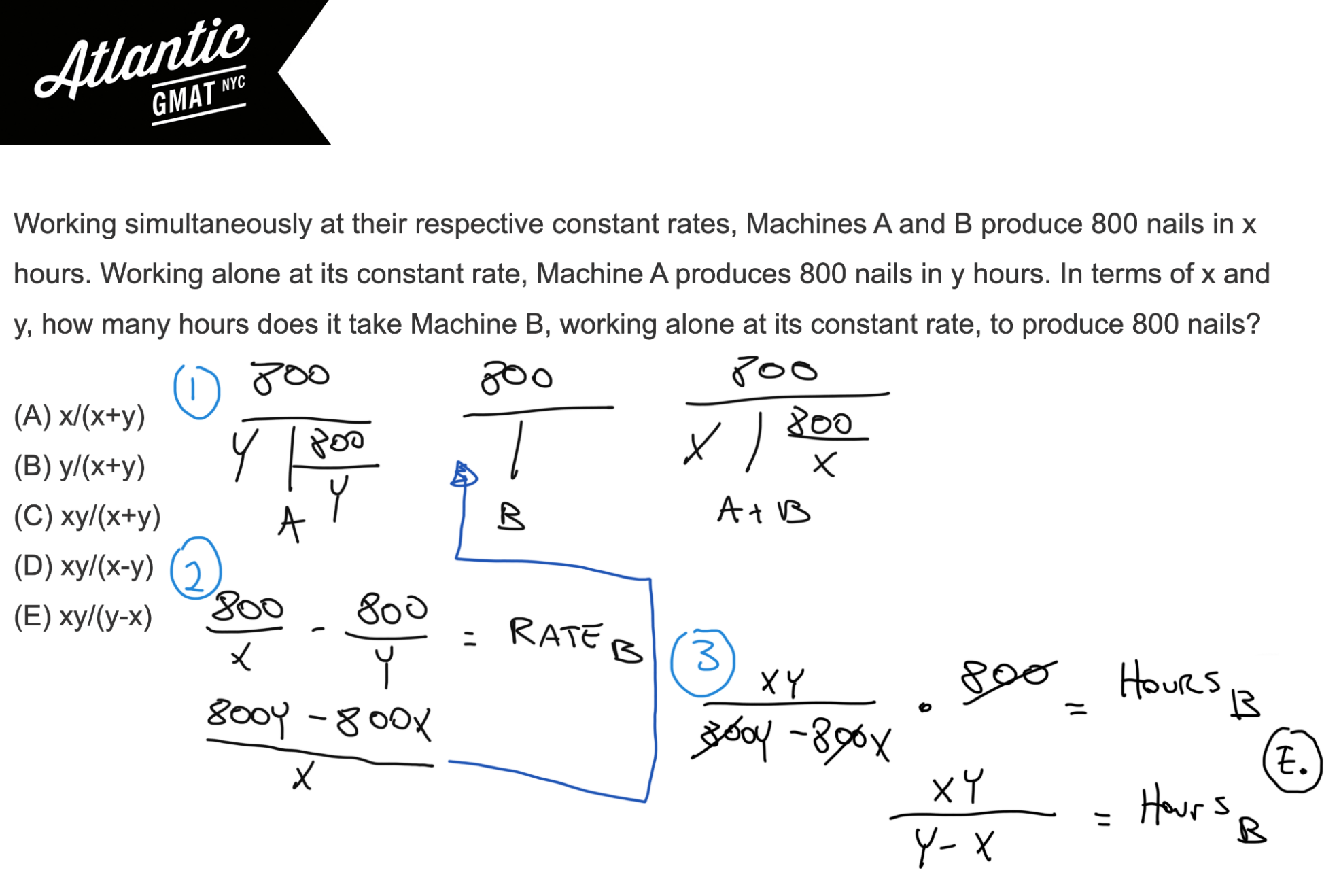
Working simultaneously at their respective constant rates, Machines A and B produce 800 nails in x hours. Working alone at its constant rate, Machine A produces 800 nails in y hours. In terms of x and y, how many hours does it take Machine B, working alone at its constant rate, to produce 800 nails?
(A) x/(x+y)
(B) y/(x+y)
(C) xy/(x+y)
(D) xy/(x-y)
(E) xy/(y-x)
Working simultaneously at their respective constant rates. Ring a bell? It should. If machines/people/whatever are working simultaneously it is almost certain you are dealing with a cooperative rate question.
Ok, let’s define the question: How many hours does it take Machine B, working alone at its constant rate, to produce 800 nails? So we want Machine B’s hours.
Are there any complicating factors here? Well, sort of. You have a bunch of variables to deal with. Machine A’s and total rate are defined by y and respectively. Don’t panic. That’s OK. Treat variables as you would treat numbers. They behave the same way in most circumstances.
Let’s start solving this with the variables and then, because we have variables in the answers and it seems like it could be a good strategy here, let’s try picking numbers.
Set up three T’s. One for each machine and one for the machines working together. Fill in the 800 nails for all three T’s and add the x and y hours into the time slots for the cooperative rate T and for Machine A’s T. How can we derive Machine B’s hours? You have the total rate/coop rate and A’s rate. A’s rate + B’s rate = Total Rate/Coop Rate. So Total – A = B. Bingo! Subtract the part (A) from the total (A + B) to get the other part (B). Once we have B’s rate we can solve for B’s time (since we already have the job/work, 800 nails. All of the computation is in the diagram below.
The other way to do this and my preferred solution is to pick numbers. Again, how do you decide whether it’s worth picking numbers? Ask yourself: If I had the numbers (instead of the variables) would solving for Machine B’s hours be easy? The answer here is a resounding YES! Why? Well, you would just have to plug the numbers into the rate T’s and voila, you’d be done. OK – great!
So what numbers to pick… We need to define x, y, and B’s hours keeping in mind that the hours it takes each machine to do the job is directly related to the hours it takes them to do the job together. To make life very easy I would make the time each machine takes to produce 800 nails the same. The numbers you pick don’t really matter but choose integers and keep them on the smaller side because you’ll plugging back into the answer choices.
What if y is 2. Machine B hours also 2. What is x (hours working together)? If they take the same time then they have the same rate. Meaning if you have two of them the rate is doubled and the time is halved. So x (total time with machines working together) is 1. That’s it. Plug in 1 and 2 for x and y respectively and the correct answer will yield 1. It’s that simple. Basically no calculations involved.
Correct Answer: E
Video Solution: Working simultaneously at their respective constant rates, Machines A and B produce 800 nails in x hours. Working alone at its constant rate, Machine A produces 800 nails in y hours. In terms of x and y, how many hours does it take Machine B, working alone at its constant rate, to produce 800 nails?
Additional GMAT Cooperative Rate and Picking Numbers Practice Questions
This is a slightly oddball work and rate question from the GMAT Official Guide that feels very different than the above and is tougher but, in my mind, tests a lot of the same skills.
Here’s another work and rate question but it’s an average rate. Though you’ll still use rate T’s the setup is a bit different. That said, it’s a good one to review for picking numbers practice: During a trip, Francine traveled x percent of the total distance at an average speed of 40 miles per hour
And a very typical but tough cooperative rate question from the GMAT Prep Tests. These come up so important to know the style:
This is a cooperative rate from GMAT question of the day. You can practice your rate T’s and sharpen your understanding of cooperative rate.
And another cooperative rate example from question of the day. This one uses proportions instead of real numbers so gives you another opportunity to practice picking numbers.
This GMAT question of the day is a bit more of a work/rate puzzle but the basic components are the same. Though it seems a bit non-standard you do see this variation a bunch so it’s important to practice.
And just for some balance here’s a Data Sufficiency Cooperative Rate question.
And lastly a GMAT Question of the Day cooperative rate question with a constraint.