Mary passed a certain gas station on a highway while traveling west at a constant speed of 50 miles per hour. Then, 15 minutes later, Paul passed the same gas station while traveling west at a constant speed of 60 miles per hour. If both drivers maintained their speeds and both remained on the highway for at least 2 hours, how long after he passed the gas station did Paul catch up with Mary?
A. 30 min
B. 45 min
C. 1 hr
D. 1 hr 15 min
E. 1 hr 30 min
Here’s a typical GMAT work and rate question from the GMAT prep tests 1 and 2. You should be psyched to see one of these on your GMAT as they are very formulaic (unlike many other GMAT questions).
We see the Mary/Paul/Gas Station question (and others like it) pretty often in tutoring sessions because of the missing distance that you need to infer from the time (more on that below). It’s just a little wrinkle but throws people off. Luckily it doesn’t require much brain or math power to figure it out and once you see it you should be able to spot it in other questions.
The key to work and rate is understanding all of the moving parts so the inferences are easier to see. If there’s anything confusing about how the different pieces of a work and rate question interact really dig in until you’ve got it all figured out.
Here at Atlantic we like to organize work and rate information in T charts as the charts make it easy to:
- See what information you have and what is missing
- Make inferences
This question is so calculation/inference light that the T’s don’t end up doing much but I think they’re still helpful.
Let’s start from the end and define the question: How long after he passed the gas station did Paul catch up with Mary?
Table of Contents
OK, so we have a catch up question with some conditions that we need to account for. A catch up question is a type of cooperative rate question. Usually with cooperative you’ll end up adding or subtracting rates in order to figure out the cooperative rate. And then often you’ll be using that cooperative rate to solve.
Let’s get the info organized
I’m going to weave a narrative here not using T’s and then add a diagram to show more of what the actual math would look like while solving.
Mary passed a certain gas station on a highway while traveling west at a constant speed of 50 miles per hour.
We have Mary’s speed (50)
Paul passed the same gas station while traveling west at a constant speed of 60 miles per hour
We have Paul’s speed (60)
What’s not clearly given is the distance that needs to be covered (how far behind is Paul?). So we need to dig a little. To find distance we need time and speed. Do we have that? Yes!
15 minutes later, Paul passed the same gas station
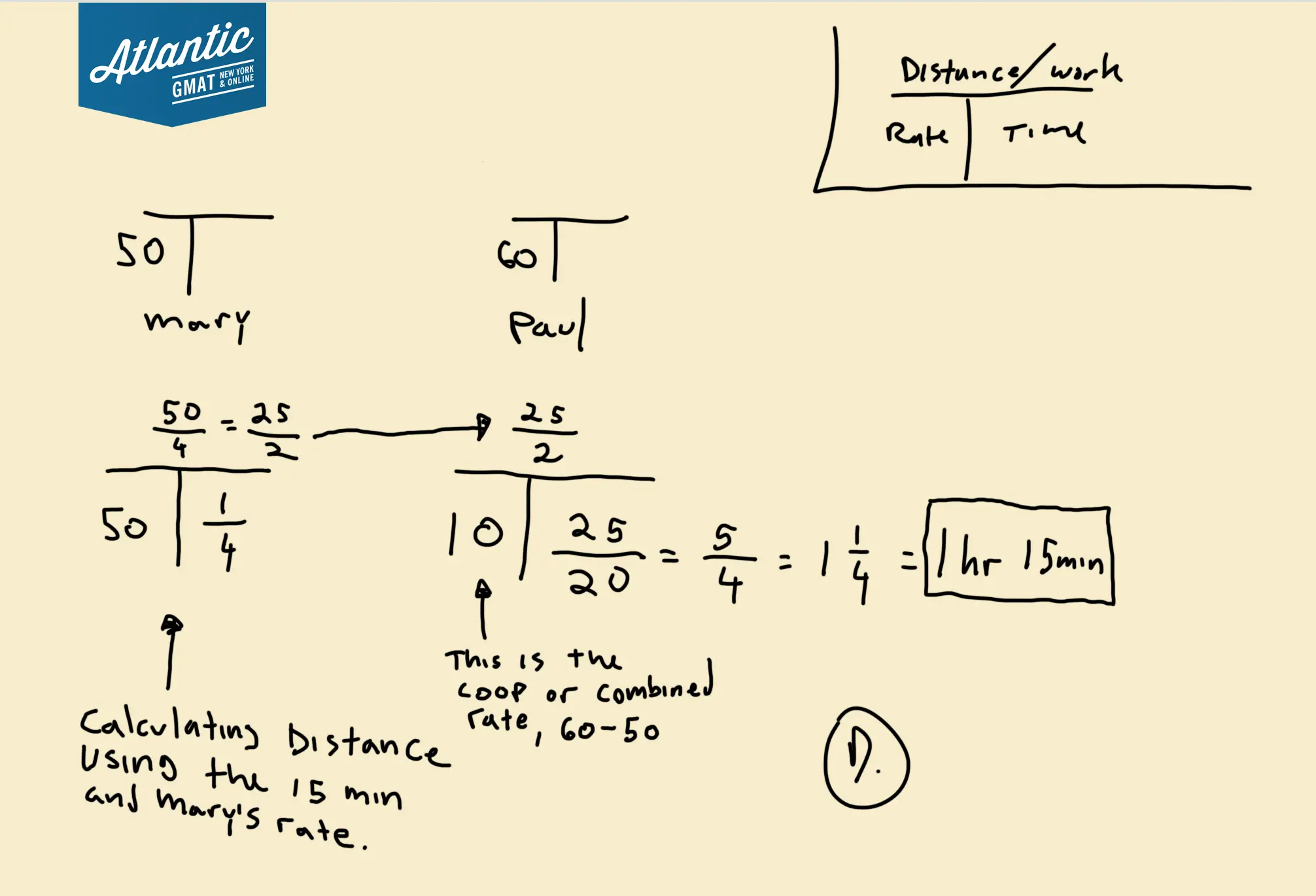
Aha! So at the point at which we’re starting to measure, Mary had traveled for 15 minutes at 50mph. Great. We have time (15) and speed (50) so we can get distance. I’d convert the 15min to hours. So 1/4 of an hour.
1/4 of an hour at 50mph gets you 12.5 miles. So Mary is 12.5 miles ahead of Paul. Now we just need to figure out how long it takes Paul to cover that distance. Remember though: they are both moving. You need to use the cooperative rate. Because it’s a catchup subtract the rates (60-50 = 10). Paul catches up at 10mph.
How long does it take to cover 12.5 miles at 10mph?
12.5/10 = 25/20 = 5/4 = 1.25 hours or 1hr 15min.
Correct Answer: D
Here is the diagram using the rate T’s to organize the information
This follows the same logic as the explanation above but is closer to how I would actually solve it on a test.
Additional cooperative work and rate example questions
This work and rate question from GMAT question of the day is extremely close in structure to the above so great practice.