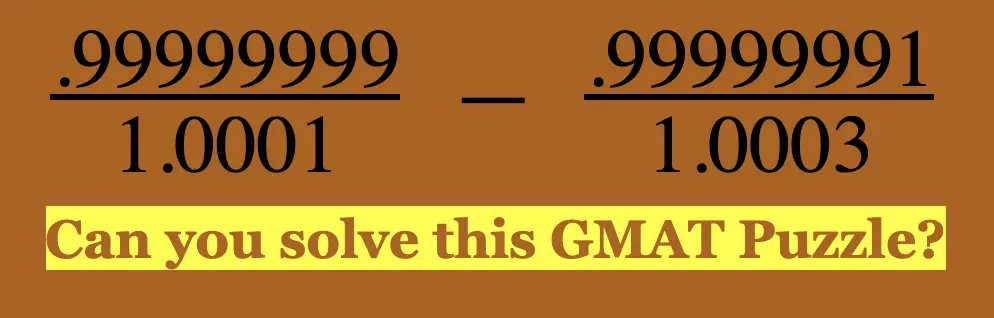(0.99999999/1.0001) − (0.99999991)/1.0003 GMAT Explanation, Video Solution, and Additional Practice!
Table of Contents
(0.99999999/1.0001) − (0.99999991)/(1.0003) =
(A) 10^(−8)
(B) 3∗10^(−8)
(C) 3∗10^(−4)
(D) 2∗10^(−4)
(E) 10^(−4)
Give it a shot on your own and then you can reference the explanation and video solution. Good luck!
This is a tough GMAT exponents puzzle from the GMAT Official Guide. I love seeing these because:
- The question type is easy to see. This .99999999 or 1.0000001… sticks out.
- Once you know the question you’re half done! And the follow through on these is somewhat formulaic.
If you follow our explanations or are a tutoring student then you know that we’re always striving to start by defining the question. In this case though there’s nothing to define. Also, there’s not much of a distinction between setting the question up and solving it.
That said, we’re going to call the initial inference the “setup” and then the number crunching/simplifying the equation the “solve”.
Setup
First off, let’s change the format of these numbers. It’s going to be a challenge working with .99999999 as is. You’re not going to be able to divide .99999999/1.00001 without a calculator and the GMAT isn’t going to expect you to do any brutal arithmetic. Again, let’s change the format. The row of 9’s should make you think about 0’s. Why? Because a long string of 0’s becomes a long string of 9’s once you subtract from those zeroes (because of borrowing). GMAT loves to use this property. Now let’s consider what we need to subtract from the nearest integer to create this .99999999. The nearest integer is 1. So we need to think 1 – ? = .99999999
Well, you guessed it, to create a 9 at the end you need to subtract a 1 at the end. You can always gives yourself a simple example to test. Think 1000 – ? = 999. 1000 – 1 = 999. So again we just need a 1 at the end. That’s it. Easy. Now translate that to our situation. How do we get a 1 at the end? 1.00000000. We need a one 8 places back so all of those zeroes turn to 9’s. So 1*10^-8. The -8 sends the 1 8 places back. Be comfortable with powers of 10, including negative powers, as you’ll be using them all over the test.
Next up, 1.0001. GMAT tutoring students usually find this one easier. 1 + 10^-4.
The second fraction we’ve got .99999991. Same thing but with a 1 at the end. So think simple: 1000 – ? = 991. Yep, 9. So instead of 1 8 places back we need a 9. 1 – 9^10-8. And, 1.0003 = 1 + 3*10^-3.
Solve
Finally all together:
(1 – 10^-8)/(1 + 10^-4) – (1 – 9*10^-3)/(1 + 3*10^-4)
What’s next? You might be thinking that this still looks complicated. Let’s look for clues!
We’ve got exponents and subtraction. We also have perfect squares.
1 is a tricky perfect square everyone forgets. Even exponents always create perfect squares. That should get you thinking about difference of squares. Foggy on that concept? Dig in. You’ll need to know difference of squares backwards and forwards to have a good chance at succeeding on your GMAT.
So 1 – 10^-8 = (1 – 10^-4)(1 + 10^-4)/(1 + 10^-4)
The entire first fraction looks like this: (1 – 10^-4)(1 + 10^-4)/(1 + 10^-4). We can cross out (1 + 10^-4) to leave (1 – 10^-4).
Let’s do the same thing with the second fraction remembering that we also take the root of the coefficients, in this case 9.
(1 – 9*10^-3) = (1 + 3*10^-4)(1 – 3*10^-4).
The entire thing: (1 + 3*10^-4)(1 – 3*10^-4)/(1 + 3*10^-4). We can cross out (1 + 3*10^-4). That leaves (1 – 3*10^-4).
Putting things together: (1 – 10^-4) – (1 – 3*10^-4)
Remember to distribute the negative sign.
1 – 10^-4 – 1 + 3*10^-4
Cross out the ones and re-arrange
3*10^-4 – 10^-4
You could factor out 10^-4 but GMAT workflow-wise you’re almost always better off recognizing like terms and adding or subtracting them. In this case the like term is 10^-4. We have 3 of them minus 1 of them so that leaves 2*10^-4. If that’s confusing just sub in the variable x for 10^-4. 3x – x = 2x. Then sub 10^-4 back in.
Again, these are great to get on your GMAT. Most other people will get this one wrong but learn the above and you’ll have a solid shot at blasting through a tough GMAT question. Here’s a diagram with the complete solution. This was done on the online GMAT whiteboard to give you sense for how that works. You can see me work through it on the whiteboard in the video solution and here’s a link to our suggestions for using the GMAT Online Whiteboard and whether to take the Online GMAT.
Correct Answer: D
(0.99999999/1.0001)−(0.99999991)/1.0003 Video Solution
Additional GMAT Exponents Puzzle Example Questions
Similar but different exponents puzzle from GMAT Question of the Day You need to think about the digits in the same way.
Here is some difference of squares practice from GMAT Question of the Day
Here is more difference of squares practice from the Official GMAT Practice Tests: If two of the four expressions x+y, x+5y, x-y, and 5x-y are chosen at random, what is the probability that their product will be of the form of , where b is an integer?
Here is a tough GMAT Question of the Day focusing on number properties and difference of squares
And a last GMAT Question of the Day example to make sure you’ve got a handle on exponents and powers of 10