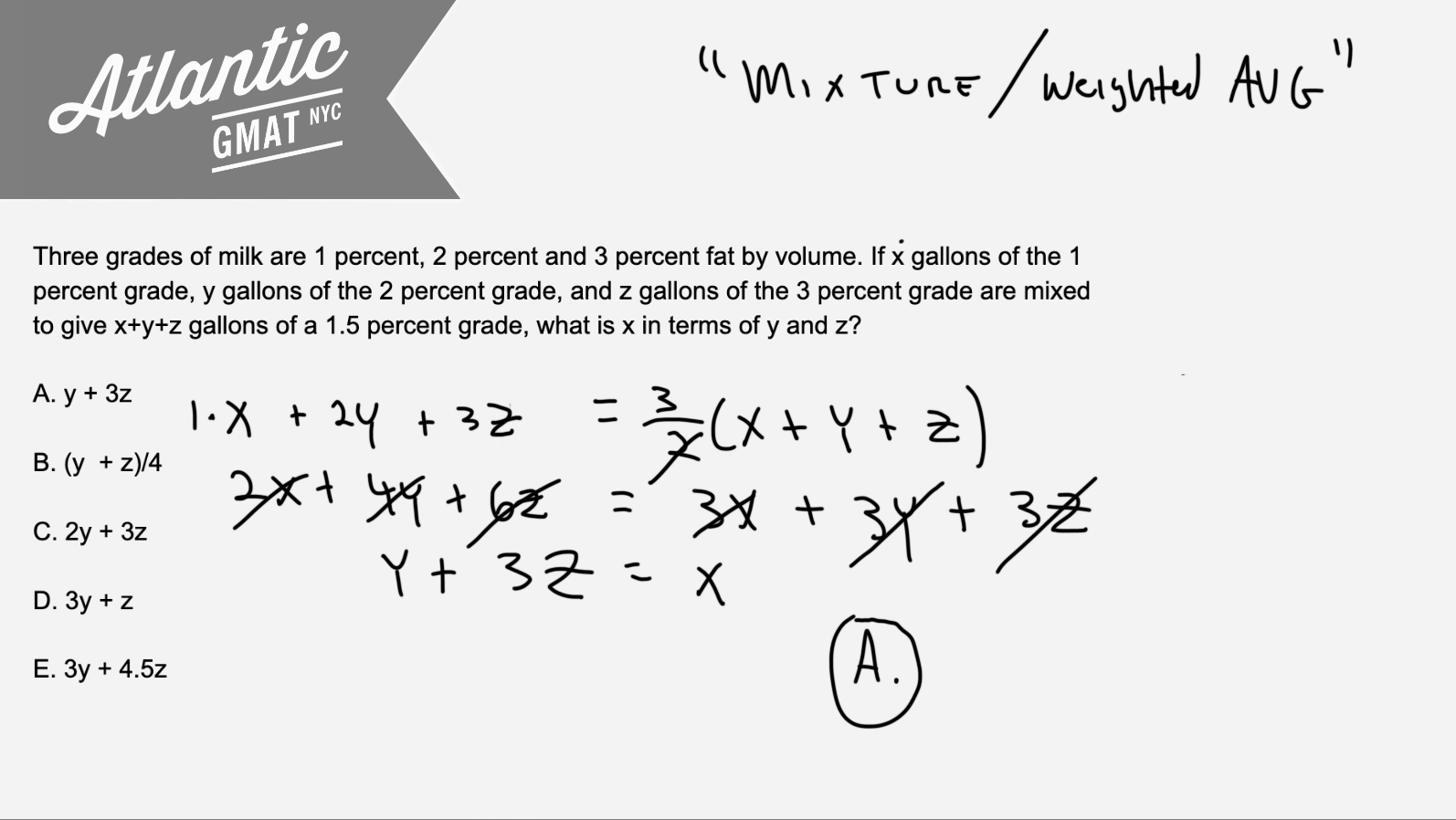Three grades of milk are 1 percent, 2 percent and 3 percent fat by volume. If x gallons of the 1 percent grade, y gallons of the 2 percent grade, and z gallons of the 3 percent grade are mixed to give x+y+z gallons of a 1.5 percent grade, what is x in terms of y and z?

Three grades of milk are 1 percent, 2 percent and 3 percent fat by volume. If x gallons of the 1 percent grade, y gallons of the 2 percent grade, and z gallons of the 3 percent grade are mixed to give x+y+z gallons of a 1.5 percent grade, what is x in terms of y and z?

(A) y + 3z
(B) (y  + z)/4
(C) 2y + 3z
(D) 3y + z
(E) 3y + 4.5z

This question is from the GMAT Prep Tests 1/2 so if you haven’t done those then hold off on this one. This is another question from the more challenging part of the spectrum that tends to come up in GMAT tutoring. The concept is basic but having variables instead of numbers tends to scare people into doing strange things.

So what is it? Weighted average! That’s it. You’ve got a certain number of gallons, x, y, and z, of three components 1%, 2%, and 3% grade milk and you’re also given the % once all of the components are mixed together (x+y+z gallons of a 1.5 percent grade).

You don’t need to solve for a number but for x in terms of y and z.

Basically: set up an equation with the given information and then isolate x (that puts x in terms of y and z). That’s it. We’ll be using the standard mixture formula but you could also get there using rate T’s that we would normally use for average rate questions.

Here’s the three grades of milk worked through

Three grades of milk are 1 percent, 2 percent and 3 percent fat by volume Video Solution

Challenging GMAT Weighted Average/Mixture Example Questions

Here’s a very similar difficult mixture question (with a bunch of variables) from the GMAT Official Guide: Seed mixture X is 40 percent ryegrass and 60 percent bluegrass by weight; seed mixture Y is 25 percent ryegrass and 75% fescue. If a mixture of X and Y contains 30% ryegrass, what percent of the weight of the mixture is X?

In the seed mixture question I show a couple of different techniques for doing weighted average/mixture questions (that you could also use on this milk question) so I would highly recommend taking a look at the post and the accompanying video.

Here’s another weighted average/mixture question from the GMAT Official Guide: Jackie has two solutions that are 2 percent sulfuric acid and 12 percent sulfuric acid by volume, respectively. If these solutions are mixed in appropriate quantities to produce 60 liters of a solution that is 5 percent sulfuric acid, approximately how many liters of the 2 percent solution will be required?