Jackie has two solutions that are 2 percent sulfuric acid and 12 percent sulfuric acid by volume, respectively. If these solutions are mixed in appropriate quantities to produce 60 liters of a solution that is 5 percent sulfuric acid, approximately how many liters of the 2 percent solution will be required?

Jackie has two solutions that are 2 percent sulfuric acid and 12 percent sulfuric acid by volume, respectively. If these solutions are mixed in appropriate quantities to produce 60 liters of a solution that is 5 percent sulfuric acid, approximately how many liters of the 2 percent solution will be required?

A) 18
B) 20
C) 24
D) 36
E) 42

You’re going to make your GMAT prep life easier by having weighted average absolutely perfected. These questions are very very very very formulaic.

Also, note that they are the same as average rate questions and can be approached successfully with the rate T’s.

We’ll tackle Jackie and her sulfuric acid solutions using those T’s and the balance beam method.

Define the question!

Approximately how many liters of the 2 percent solution will be required?

Always start from the end by defining what you’re looking for. Sometimes there won’t be much to write down but it’s always a good exercise. In this case we’re looking for liters of the 2% solution.

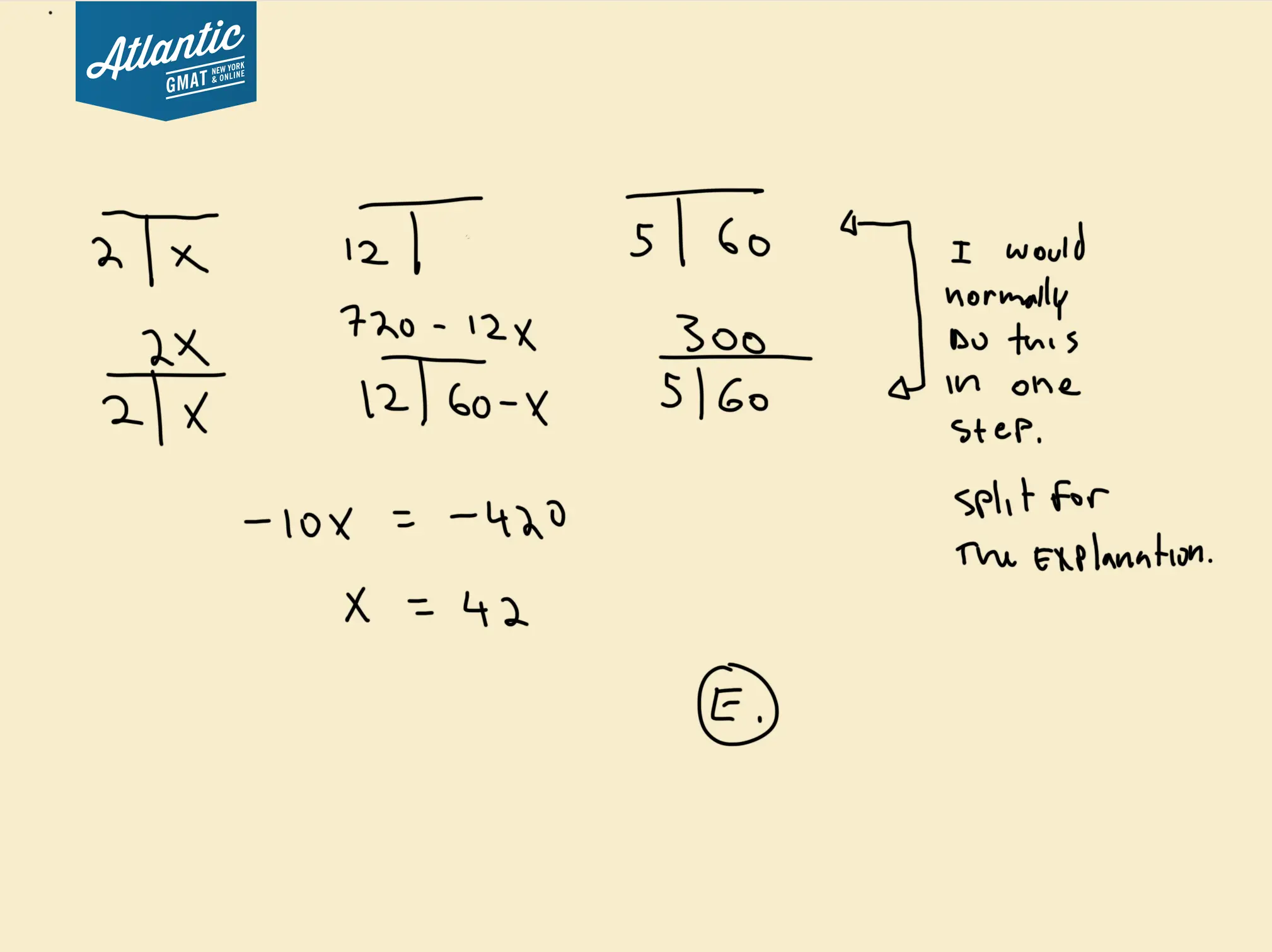
Jackie has two solutions via Average Rate T’s

As we agreed above, mixtures are the same as average rate questions and can be solved using T’s.

The only tricky thing is figuring out what to put where because the components of a mixture question are different than the components of a rate/work question. So we need to map our mixture components onto the T system so they make sense.

Here are some tips for making this easy:

Rate: Whatever you put in the rate box much a value that CANNOT be summed with any other values

Time: Whatever you put in the time box must be something that you can add to sum to a total.

Work/Distance: Whatever you put in the work/distance box must be the product of two things and also must be something that can be added to a total.

The 2%, 12%, and 5% don’t add up so must go in the rate box.

The 60 liters isn’t a product so must go in the time box.

What about the other boxes? Well, you need a variable. So pick one for what you’re solving for (how many liters of the 2 percent solution will be required). Let’s call the liters of the 2% solution x.

Now let the T’s do their magic. You can see that 60 (total) – x must equal the 12% solution. Now take the product of each box to get the work/distance box filled in and solve for the equation up top.

Here is all of that worked out:

Jackie’s Acid on the Balance Beam

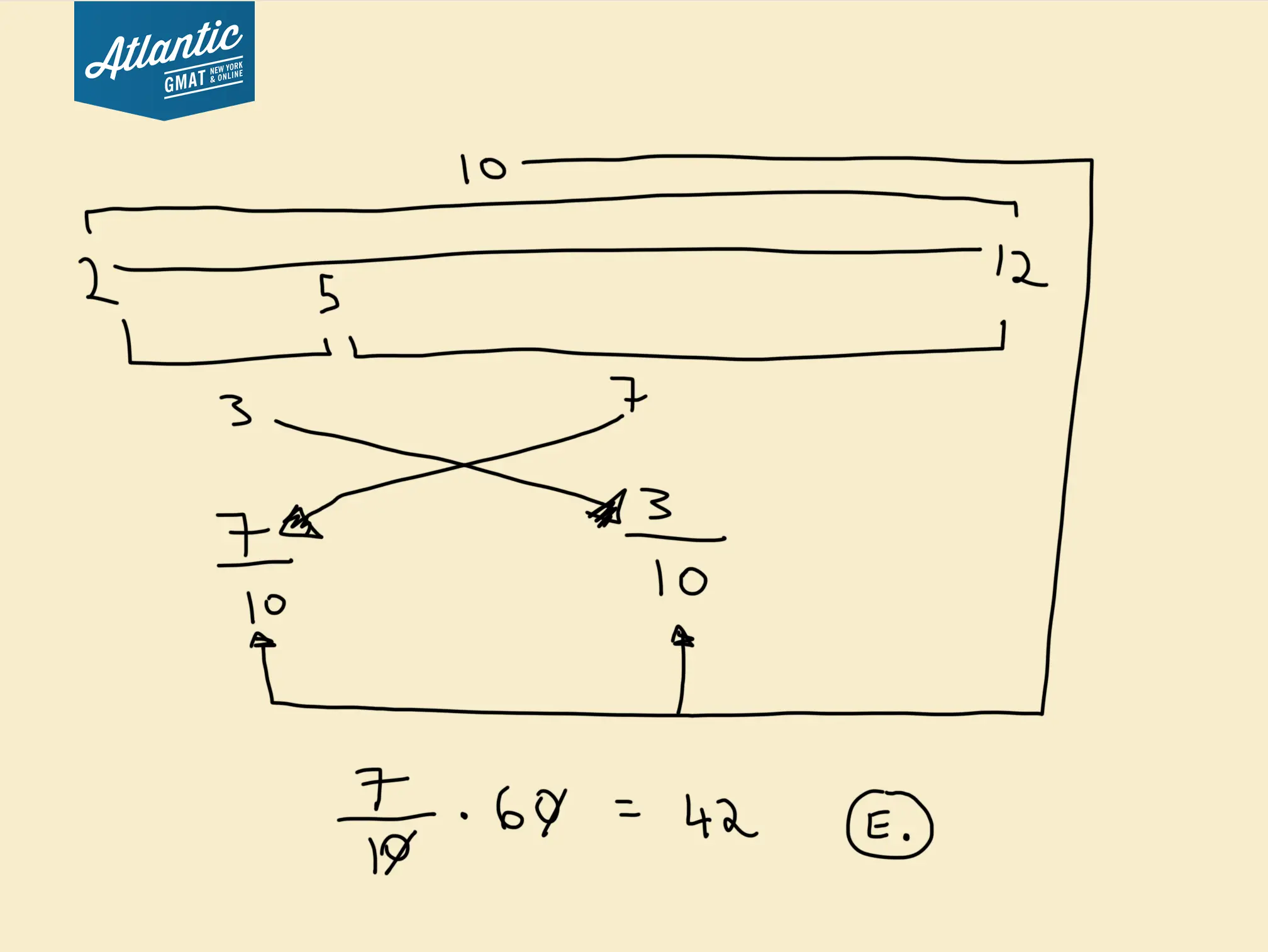
The balance beam works really well on mixture questions because on mixtures you tend to get the rate information which is exactly what you need for the balance beam.

2——-5————————12

Out the rates on the line with the “total” rate approximately where it should sit (it’s closer to 5 so that’s where I put it). Then take the difference of each part and the total: 5-2 = 3 and 12-5 = 7. Then take the difference of the two parts, 12-2 = 10.

Create two fractions with that second difference, 10, as the denominator for both and 3 and 7 as numerators.

3/10, 7/10

That’s it. 7/10 represents the proportion of the solution that is 2% sulfuric acid and 3/10 represents the portion of the solution that is 12% sulfuric acid. Since we 60 gallons total, 7/10 * 60 = 42.

So we have 42 gallons of 2% solution and 18 gallons of 12% solution.

And that makes sense since 5 is much closer to 2 than 12. So more of the solution must be 2%.

That’s also a quick way to eliminate answer choices. We know that there’s more of the 2% so there must be more than 30 gallons of 2% (more than half of the 60 gallon total). So A, B, and C are out. And between D and E, it looks like D is too close to 30 considering how much farther away 12 is from 5.

Here’s the sulfuric acid balance beam worked out

Correct Answer: E

Additional GMAT Weighted Average/Mixture Practice Questions

Here’s a great one from the GMAT Official Guide. Same principles as Jackie’s sulfuric acid solution. You can use the T’s, balance beam, or mixture/weighted average formula: Seed mixture X is 40 percent ryegrass and 60 percent bluegrass by weight; seed mixture Y is 25 percent ryegrass and 75 % fescue. If a mixture of X and Y contains 30% ryegrass, what percent of the weight of the mixture is X?

Another challenging mixture question from the GMAT Prep Tests. This one presents a whole bunch of variables. You can’t use balance beam because you have more than two components to the mixture but you can use T’s or weighted average formula: Three grades of milk are 1 percent, 2 percent and 3 percent fat by volume. If x gallons of the 1 percent grade, y gallons of the 2 percent grade, and z gallons of the 3 percent grade are mixed to give x+y+z gallons of a 1.5 percent grade, what is x in terms of y and z?