The number 75 can be written as the sum of the squares of 3 different positive integers. What is the sum of these 3 integers?

The number 75 can be written as the sum of the squares of 3 different positive integers. What is the sum of these 3 integers?

(A) 17
(B) 16
(C) 15
(D) 14
(E) 13

This question is from the free official GMAT practice tests 1 and 2 so avoid if you haven’t done those already.

Define the question: What is the sum of these 3 integers?

Not much to define but I’d maybe write out: X + Y + Z = ? to represent the sum.

Setup

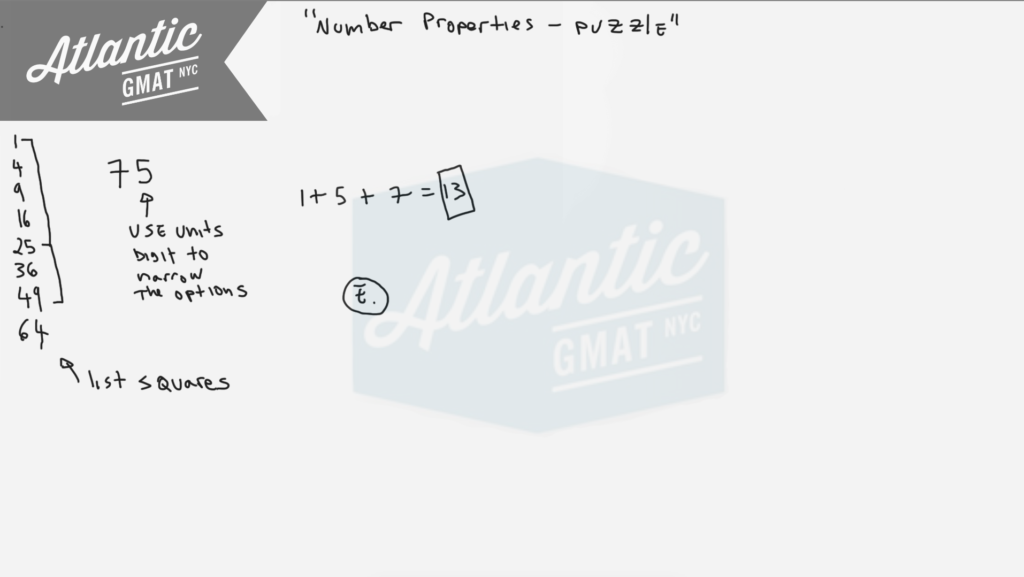
Most of this question is in the setup. Look for something to organize: The sum of the squares of the 3 different positive integers sum is 75. OK. So go ahead and list the first bunch of squares starting from 1 up to just below 75. Once you’ve got that you just need to find the combination that works.

1

4

9

16

25

36

49

64

81 (TOO BIG)

Solve

Before you start writing like crazy come up with a mini-plan. Is there anything in the question to guide your work? In this case let’s look at the constraints:

75 can be written as the sum of the squares of 3 different positive integers

We need to sum to 75 so let’s start from the bigger integers (that will take up more of that space) and work down to fill in what’s left over. Why? To get to 75 you’re going to need one of those big guys (64, 49, or 36).

Finding a constraint can be very helpful. Usually with these GMAT puzzles there are little shortcuts. Generally you don’t pull them out of thin air. They are the natural conclusion of good organization. Make sure to take your time with setup so you pave the way for success. Here’s another GMAT question that relies on just staying organized and paying attention: For a certain race, 3 teams were allowed to enter 3 members each. A team earned 6 – n points whenever one of its members finished in nth place, where 1 ≤ n ≤ 5. The details are very different but the style is similar and I think it requires the same kind of thinking.

OK, back to solving!

Starting with 64.

64 + ? = 75

We need 11 to reach 75. So look at your list and see if the sum of any of the two integers equals 11. Not possible. 64 is out.

Let’s do the same thing with 49.

49 + ? = 75

We need 26. Scan the list. Bingo: 25 + 1. Easy.

We need the sum of the squares of those so 7 + 5 + 1 = 13.

What is the sum of these 3 integers? 13. E. 

Takeaways

-Do basic organization. Make list, make a diagram, make a chart… Do something with information given. From simple setup come more complex inferences.

-Focus on constraints or whatever parameters you can in the question to guide your follow through. Always try to come up with a mini-execution plan!

Video Solution: The number 75 can be written as the sum of the squares of 3 different positive integers. What is the sum of these 3 integers?

Additional GMAT Number Properties, Puzzle, Constraints Practice Questions

As mentioned above this questions has a very similar vibe in terms of the basic organizing and using constraints to solve: For a certain race, 3 teams were allowed to enter 3 members each. A team earned 6 – n points whenever one of its members finished in nth place, where 1 ≤ n ≤ 5.

Here’s another GMAT puzzle that is a bit different but can also be solved with a similar style of basic organizing: If x and y are positive integers such that y is a multiple of 5 and 3x + 4y = 200, then x must be a multiple of which of the following?

Here’s a challenging question from the GMAT prep tests 1 and 2 that requires a similar set of tools: If each term in the sum a₁ + a₂ + a₃ +…+ a_n is either 7 or 77 and the sum equals 350, which of the following could be equal to n?

And here’s a puzzle from GMAT Question of the Day that also benefits from just getting the info from the question in shape.