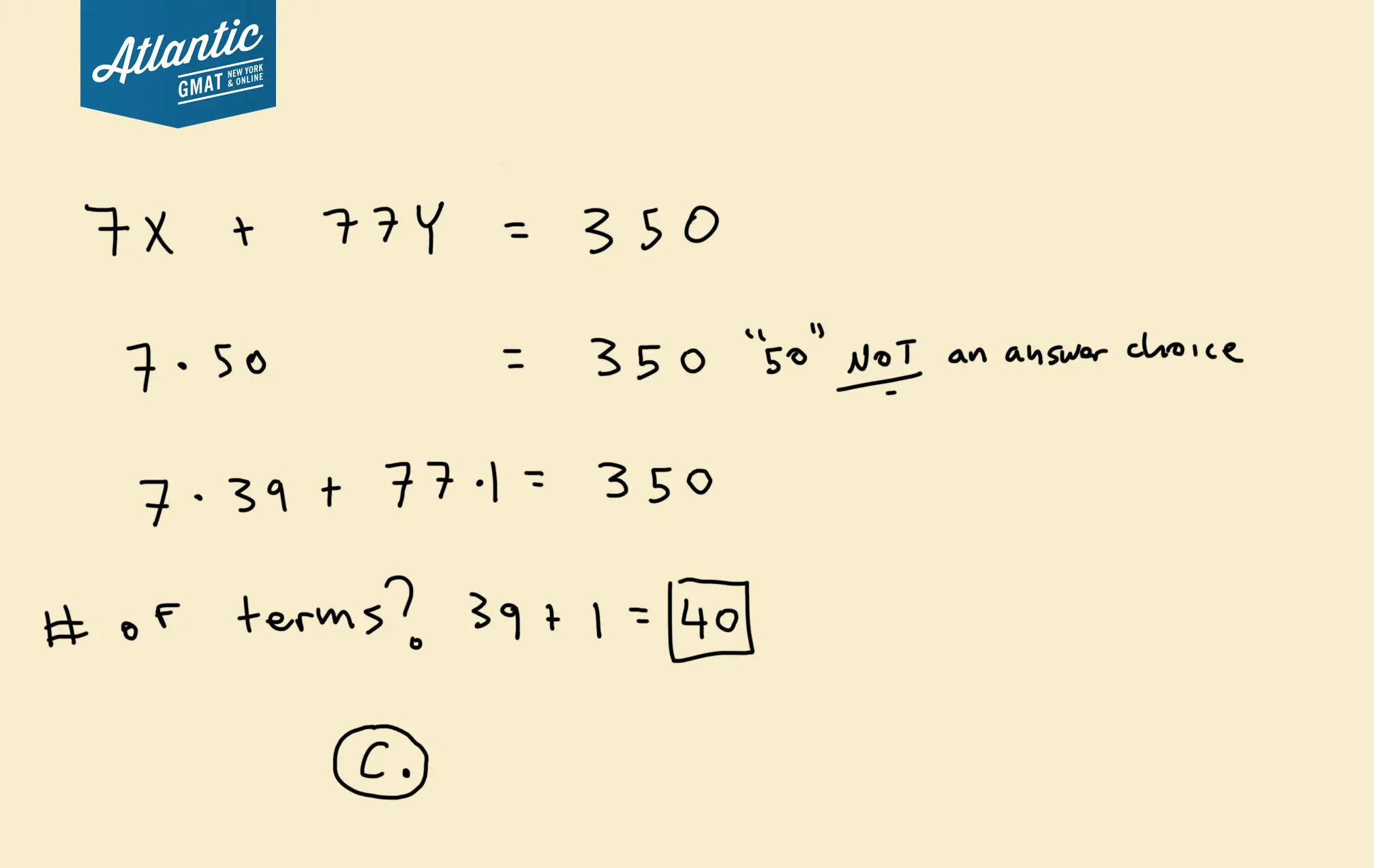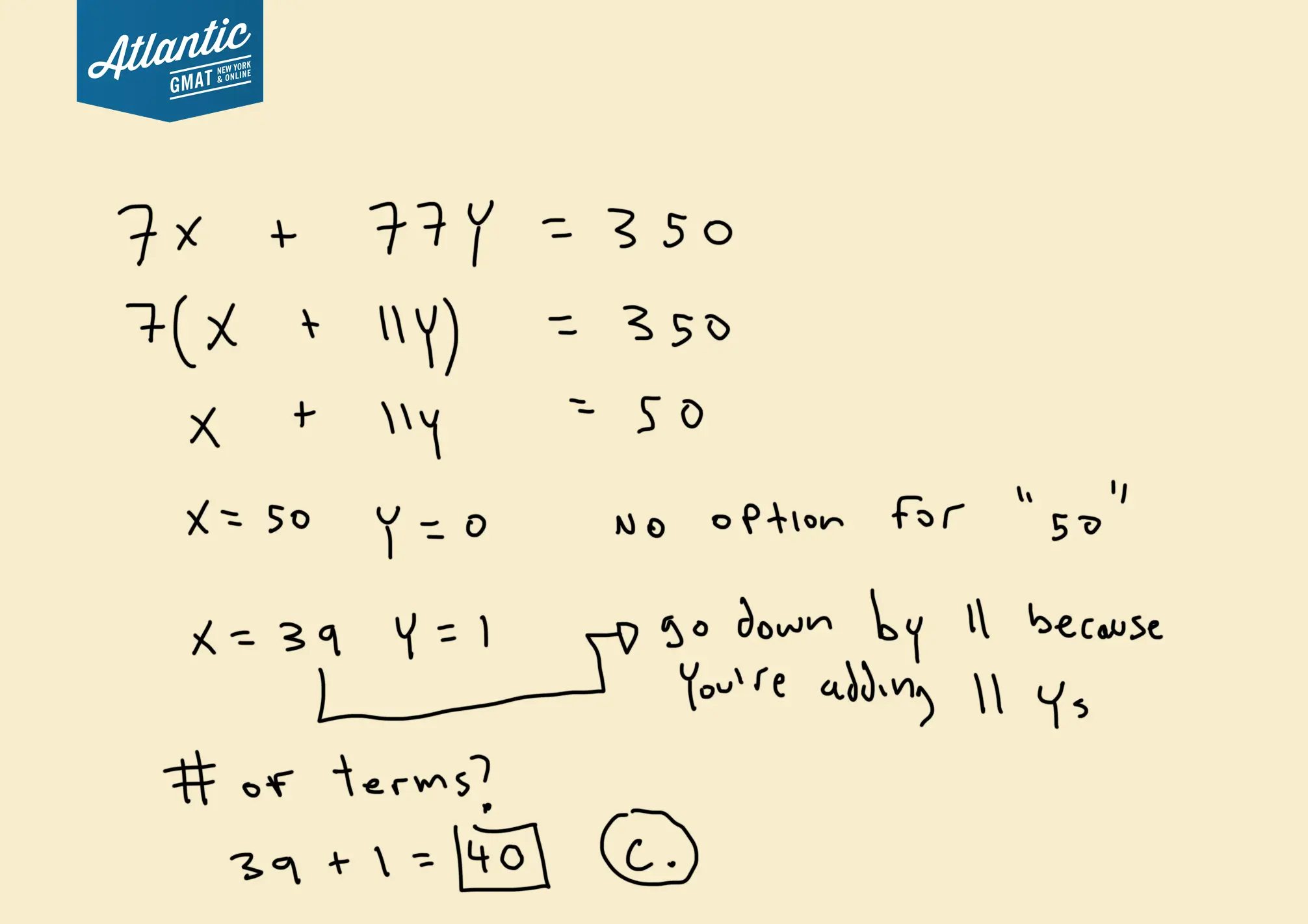If each term in the sum a1 + a2 + a3 +…+ an is either 7 or 77 and the sum equals 350, which of the following could be equal to n?

A. 38
B. 39
C. 40
D. 41
E. 42

Stumped by this GMAT sequence puzzle from the GMAT Prep tests 1 and 2? We’ve got you covered!

We’ll do a quick overview on sequences so you have a sense for what this means: If each term in the sum a₁ + a₂ + a₃ +…+ a_n

We’ll also provide some general strategy for sketching out any puzzle question that doesn’t have an obvious framework.

GMAT Sequences

OK – so what are sequences? They’re a set of numbers that follows a certain pattern. That’s it.

The subscript (for a₁ I’m talking about the 1) denotes the placement of that number within the sequence. So a₁ is the first number in the sequence. a₂ is the second. a₇ would be the 7th.

a_n is the one that confuses people. That just means the “nth” spot whatever you define n as. So, if n is 10 then it’s a₁₀. If n is 21 it’s a₂₁.

I like this graphic from the sequence page on wikipedia:

Define the question

As usual let’s get the question figured out: Which of the following could be equal to n?

Easy enough but let’s think about what that means.

The “n” in is the last terms in this sequence. So we’re looking for what the total number of terms could be given constraints: the sum a₁ + a₂ + a₃ +…+ a_n is either 7 or 77 and the sum equals 350.

Since there are multiple possible values of n make sure to use the answer choices to help narrow things down.

Organize the information

Now let’s get those constraints organized.

Some of the numbers will 7’s

Some of the numbers will be 77’s

and the sum of the numbers is 350.

OK, so let’s add some variables for the things we don’t know and set up an equation.

7x + 77y = 350.

One equation but two variables. So that’s not quite solvable with algebra. However, with certainty there are sufficient constraints that force x and y to be specific numbers (or else this question wouldn’t work).

How can you get the constraints working for you?

Be practical. Start considering what x/y values would work and maybe even what wouldn’t work. Again, especially for a “could” I’d always check the answer choices for clues.

Here they help a ton because they indicate that we must have a whole bunch of 7’s. Why? Well, even at the low end of the answer choices we have 38 terms. Most of those have to be 7’s or else the sum would be much greater than 350 (you can’t have than 4 77’s before overshooting 350).

I’d make a chart starting from as close to 350 as possible using 7’s:

7*50 = 350

Now let’s start adding in 77’s and look for combinations that work.

7*39 + 77 = 350

That works. One and done!

Solve

Let’s get back to our question: Which of the following could be equal to n?

How many terms do we have? 39 (7) + 1 (77) = 40.

Correct Answer: C

Here’s all of that summed up in a diagram:

Alternate Solution

There’s another way to organize this one and it’s worth pointing out because it highlights a good GMAT habit: factoring!

Let’s start from the equation we defined: 7x + 77y = 350

Notice the 7 and 77. It’s almost always the case that factoring will help you on the GMAT. So let’s try to pull out the 7.

7(x + 11y) = 350.

x + 11y = 50

That’s kind of nice. The numbers are smaller and so easier to deal with.

From there you can do the same thing we did above but with these shrunken numbers.

You still have to keep in mind that the answer choices are hovering around 40 so we need many more x’s than y’s. So maximize your x’s first.

You could have 50 x’s but that’s not an answer. Let’s start with the next interval down:

39 x’s and 1 y. So 39 + 11 = 50.

Of course that works (as it did in the first solution). And again we have 40 terms (39 7s and 1 77).

More GMAT Sequence Questions and Related Puzzles

Here’s a similar but different algebra/divisibility question from the GMAT Official Guide:

If x and y are positive integers such that y is a multiple of 5 and 3x + 4y = 200, then x must be a multiple of which of the following?

Another example that uses a similar skill set from the GMAT Prep Tests 1 and 2:

The number 75 can be written as the sum of the squares of 3 different positive integers. What is the sum of these 3 integers?

And finally here’s a GMAT Question of the Day sequence and divisibility puzzle that’s very similar to the one above.