GMAT Explanation, Video Solution, and Additional Practice Questions!
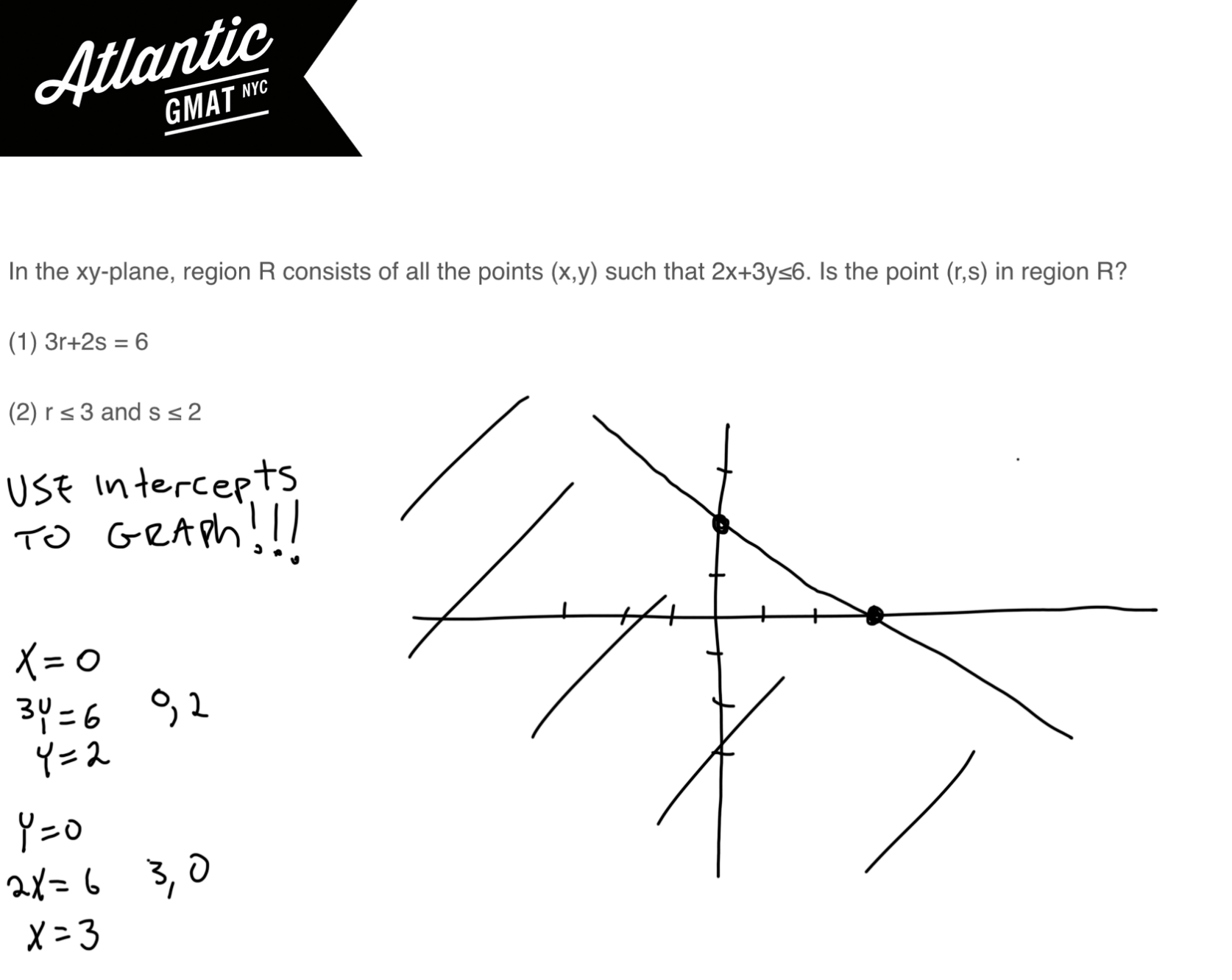
In the xy-plane, region R consists of all the points (x,y) such that 2x + 3y ≤ 6. Is the point (r,s) in region R?
(1) 3r + 2s = 6
(2) r ≤ 3 and s ≤ 2
This is a tough one and it’s rare that one our GMAT tutoring students, even the quant inclined, get this right on the first shot. First, read carefully and figure out the question. You might ask yourself: I’ve got x,y in the inequalities but r,s in the question. What’s that about? Well, r,s correspond to x,y. r = x, s = y. Easy. Basic idea, we need to see if r, s is within the graph’s boundaries. In the statements we’re given constraints that we need to account for.
Let’s go ahead and graph the given inequality. Use the x and y intercepts (make x = 0 then make y = 0). If you need a refresh here’s a Khan video on graphing inequalities.
2x + 3y ≤ 6
That’s really half the battle right there as, again, you’ll just be plotting points to see if you’re in or out of the graph’s boundaries.
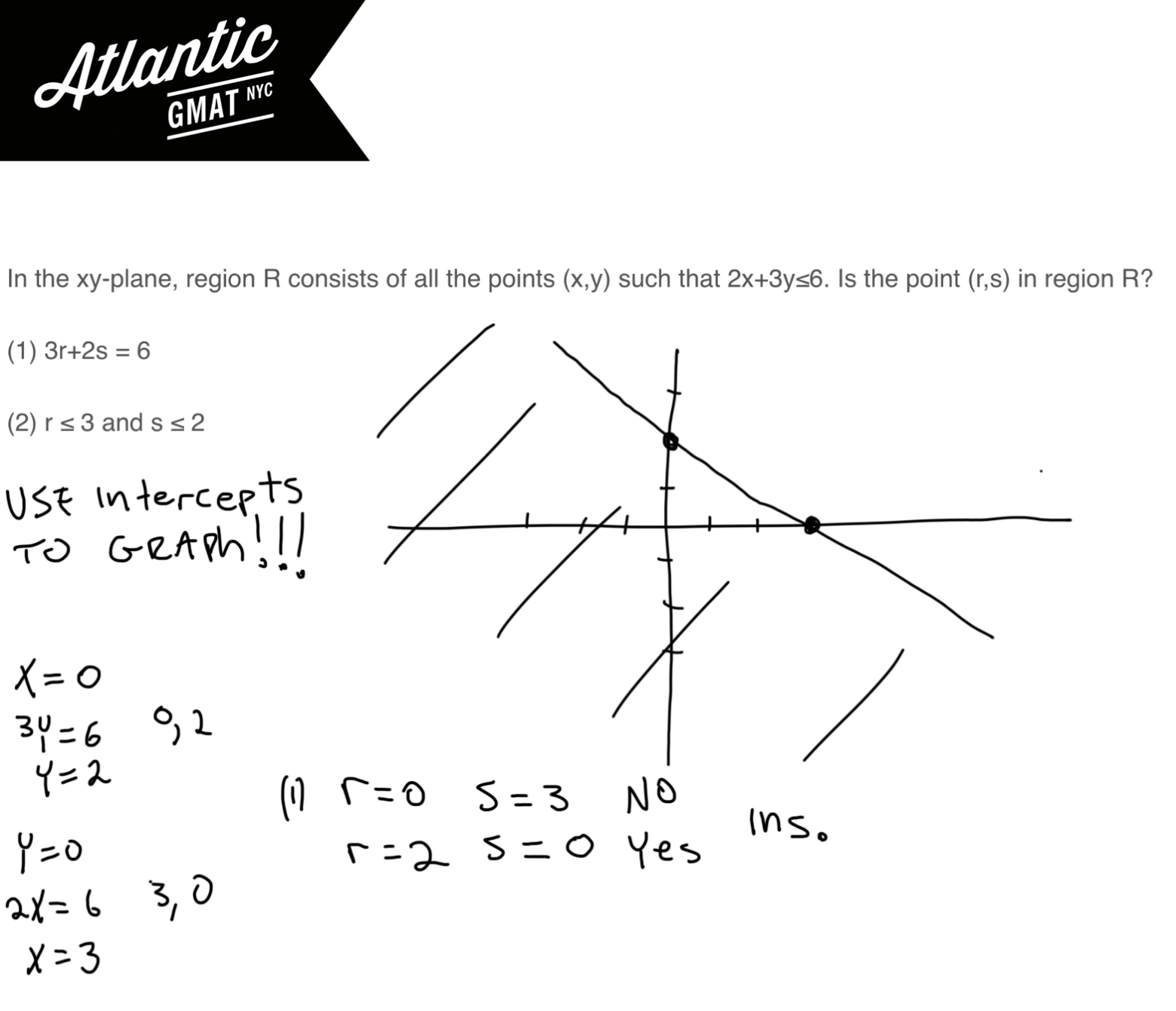
So let’s start with statement (1) 3r + 2s = 6.
Use easy numbers. Make r = 0 then s = 3. 0,3 is outside of the graph (region R) so that gives us a “no”. Now let’s try for a “yes”. Let’s try just flipping things around making s = 0 so r = 2. That’s on the graph so we also have a “yes”. That makes statement (1) insufficient.
We can follow the same procedure for statement (2), trying to prove a “yes” and a “no”.
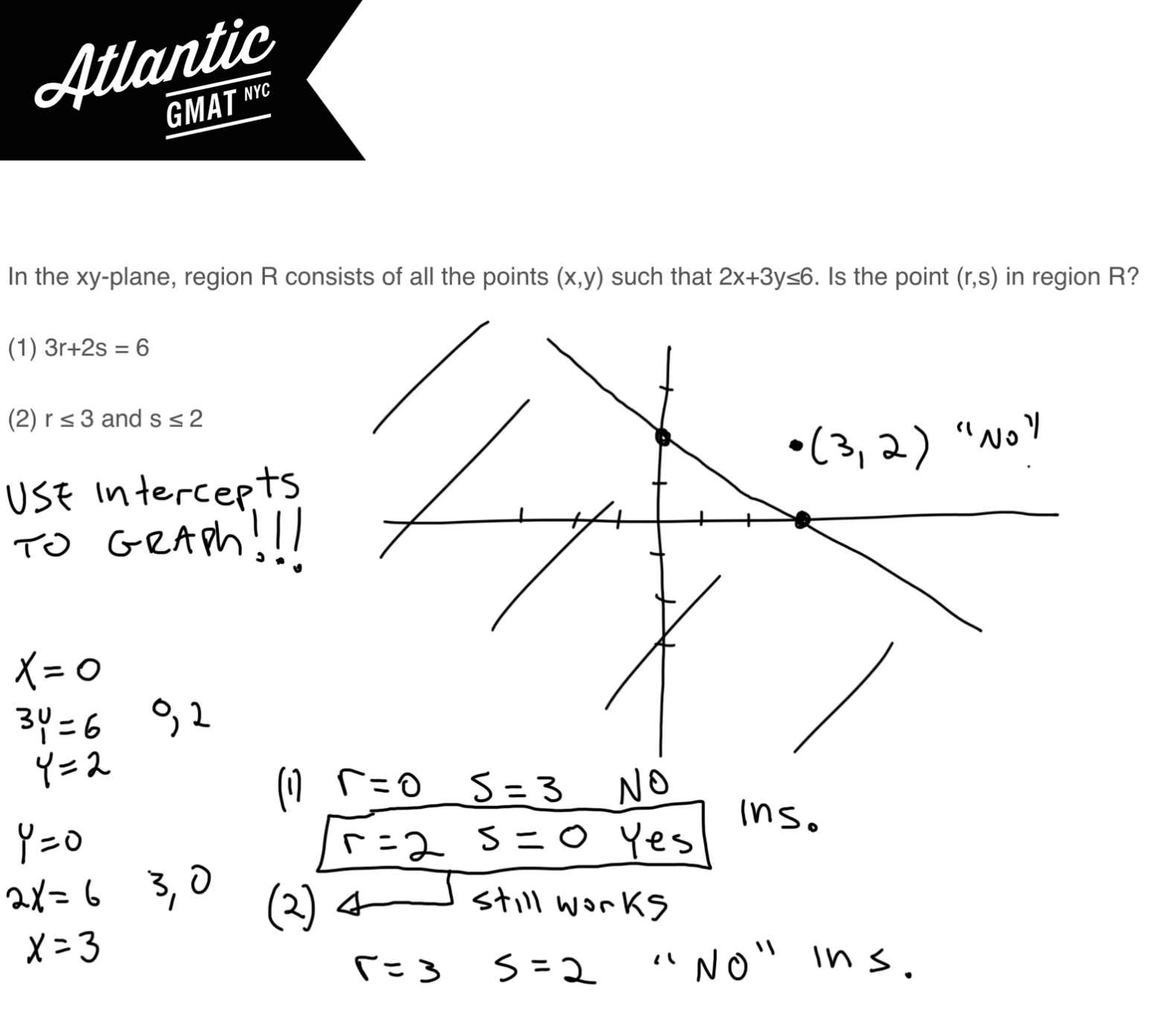
(2) r ≤ 3 and s ≤ 2
Try to re-use examples from the other statement as that tends to save time. We can still use our “yes” with s = 0, r = 2. Our “no” won’t work because s ≤ 2. So we need to consider whether we can create a know given this constraint.
Why not just try the upper limits to try to push out of the graph? r = 3 s = 2. Clearly outside of the graph so we have a “no”. That makes statement (2) insufficient.
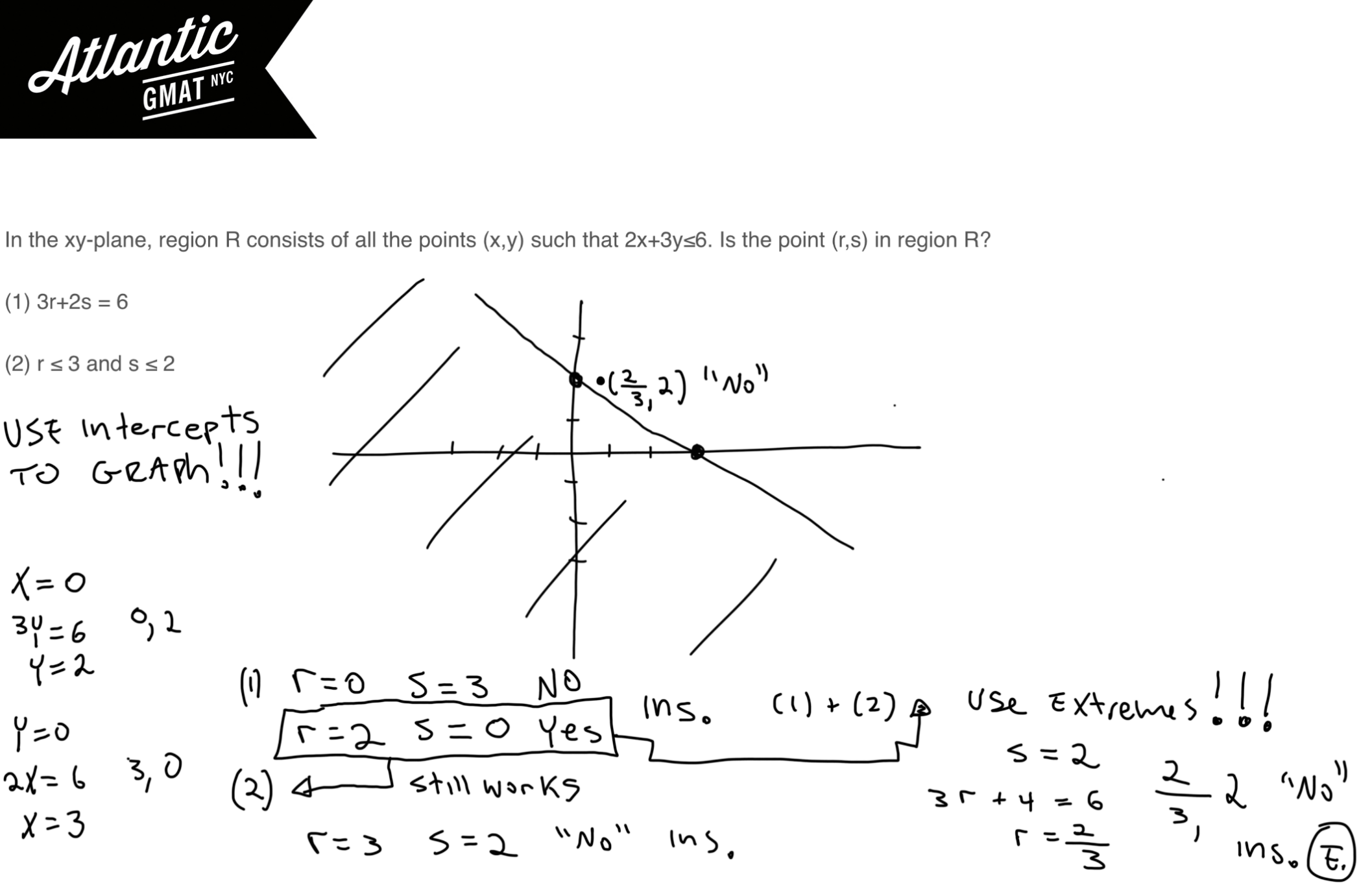
Let’s put the statements together and, if possible, reuse your examples that satisfy both statements.
(1) 3r + 2s = 6
(2) r ≤ 3 and s ≤ 2
We can still use our yes example because it fit both constraints, s = 0, r = 2. Now we need to think about a “no”. Think easy. Again, I would aim for the extremes and see where that takes us. Let’s make s = 2, the upper limit for s, and see what happens. r = 2/3. Looking at the graph it’s clear that with r = 2/3 that s = 2 is out of bounds giving us a “no”. Even with both statements we’re insufficient.
A few big picture GMAT strategies to consider:
- Yes/No for Data Sufficiency. This is a biggie. Yes/No is a critical GMAT Data Sufficiency strategy. It helps you organize the question and focuses your number picking. Your goal is try to prove insufficiency!
- Sometimes GMAT tutoring clients ask: how do I know what values to pick? I get lost, end up trying out a million different options, waste a ton of time, and then just guess anyways. Use the question to help define the values. Look for endpoints or extremes. Try to consider values that will clearly fall on the “yes” or “no” side. If lost try something and consider the result.
Video Solution: In the xy-plane, region R consists of all the points (x,y) such that 2x + 3y ≤ 6. Is the point (r,s) in region R?
Additional GMAT Data Sufficiency Yes/No Practice Questions
Here’s a challenging GMAT coordinate plane question that is yes/no and has a bunch of algebra to analyze.
In the xy-plane, does the line with equation y = 3x + 2 contain the point (r,s)?
Here’s another Yes/No DS question. It’s not geometry but, again, the strategy is Yes/No so the underlying content can change but the strategy remains the same: A school administrator will assign each student in a group
Here’s a Geometry Yes/No question from the GMAT Question of the Day.
And another challenging Geometry GMAT Question of the Day
Here’s an Official GMAT Question that has very different Geometry content but uses the same Yes/No strategy: Is the area of triangular region ABC equal to the area of triangular region DBA