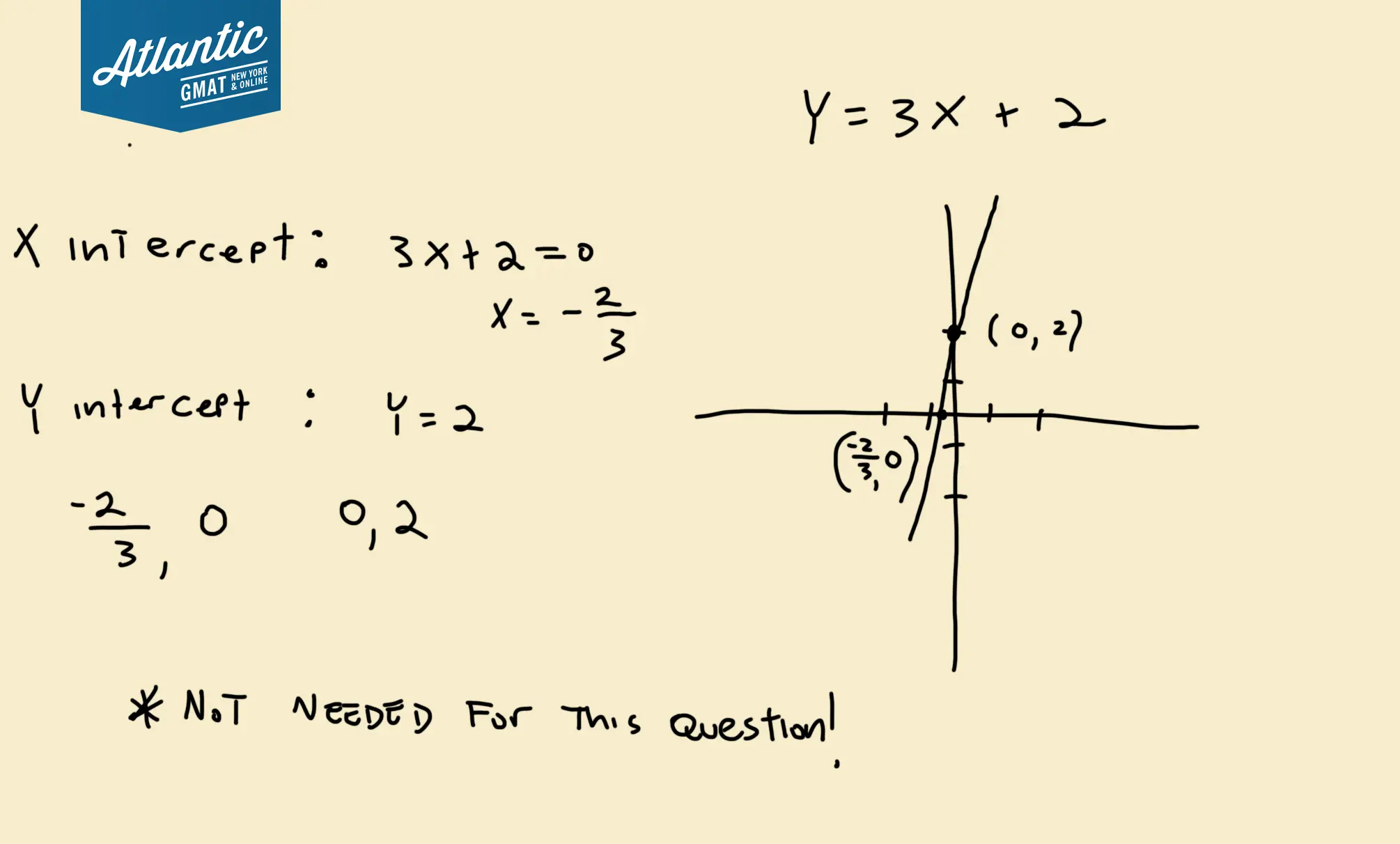(1) (3r+2−s)(4r+9−s) = 0
(2) (4r−6−s)(3r+2−s) = 0
This is a challenging geometry and system of equations/algebra question from the GMAT prep tests 1 and 2. We see this one pretty often in GMAT tutoring sessions so you’re not alone in seeking some assistance. It’s important to remember that with GMAT geometry, often, the geometry aspect is the easy part and not necessarily the real focus of the question.
Define the question: does the line with equation y = 3x + 2 contains the point (r,s)?
Table of Contents
Basically, does (r,s) sit on the line y = 3x + 2? Another way to look at it: can we substitute r in for x and s in for y? So does, s = 3r + 2? That’s what we’re looking to find out. We don’t need to solve for the individual values of r and s.
Organize the information
I probably wouldn’t make a graph. Why? Because this question is focusing on the equations/algebra. It doesn’t seem to have a spatial reasoning aspect.
Just to make sure you know how to do it: Here’s the graph of y = 3x + 2
We may not need it but for the sake of completeness a graph of y = 3x + 2. Use the x and y intercepts to make it easy.
For the x intercept make y = 0
3x + 2 = 0
x = -2/3
For the y intercept make x = 0
y = 2
So the x intercept is -2/3, 0
the y intercept is 0,2
Statement 1: (3r+2−s)(4r+9−s) = 0
It’s rare that you want to multiply out trinomials. It’s going to create a mess. What can we get from this? Either:
3r + 2 – s = 0
or
4r + 9 – s = 0
or they both equal zero.
Let’s go back to our question to see if we can match anything.
We’re looking to prove: s = 3r + 2
Is that any of these?
Yes! This is the same: 3r + 2 – s = 0
So it’s possible that r and s do sit on the line.
However they don’t have to because 4r + 9 – s could equal 0 and 3r + 2 – s could equal whatever else.
So we don’t have a definitive answer.
Insufficient.
Statement 2: (4r−6−s)(3r+2−s) = 0
Same problem here. Insufficient.
Statement 1 + Statement 2
Now things get interesting.
These equations both equal zero so equal each other.
(3r+2−s)(4r+9−s) = (4r−6−s)(3r+2−s)
Let’s bring everything over to one side so we can factor out the common term 3r + 2 – s
(3r + 2 – s)(4r + 9 – s – 4r + 6 + s) = 0
Combine like terms
(3r + 2 – s)(15) = 0
We know 15 is not equal to zero so (3r + 2 – s) must be equal to 0
3r + 2 – s = 0
re-arrange that a bit
s = 3r + 2
Look familiar?
They match. So it must be that r and s are on the line y = 3x + 2.
Alternate (and faster) solution
(3r+2−s)(4r+9−s) = 0
(4r−6−s)(3r+2−s) = 0
Let’s look at the above in a more zoomed out/practical way.
If both of those statements equal zero then it must be that 3r + 2 – s = 0.
Why?
Because one of the two parenthesis in each of the statements must equal zero.
So either 3r + 2 – s is equal to zero or BOTH 4r + 9 – s AND 4r – s – 6 must both be equal to zero.
Considering that 4r + 9 – s and 4r – s – 6 don’t equal each other (subtract them and you’ll find that the difference is 15) there’s no way that they are both equal to zero.
Here’s a very simple example of why they can’t both be equal to zero:
Can x + 1 AND x + 2 both be equal to zero? NO!!! Clearly they aren’t equal to each other so they can’t both be equal to zero. Same deal with 4r + 9 – s and 4r – s – 6
So it must be that 3r + 2 – s is equal to zero. That matches our question.
Sufficient.
Here’s everything worked out more compactly and in a more visual way
Correct Answer: C
Additional challenging GMAT Geometry, coordinate plane practice questions
Here’s another very challenging GMAT coordinate plane question that has a bunch of algebra and is a yes/no style data sufficiency question.
And another challenging GMAT coordinate plane question. Same yes/no style data sufficiency as the one the above.
In the xy-plane, at what two points does the graph of y = (x + a)(x + b) intersect the x-axis?
And here’s a more fundamental coordinate plane question from GMAT Question of the day.
Learn more about GMAT tutoring with Atlantic
GMAT Question of the Day Signup
Sign up for 1 challenging GMAT question sent to you each week.