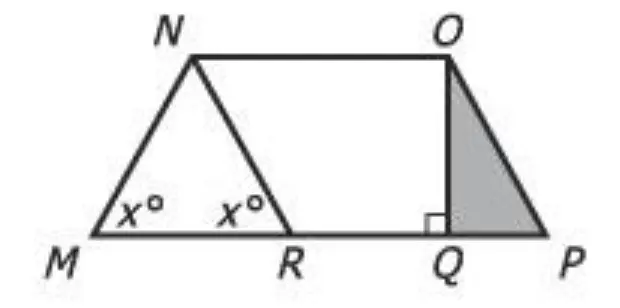
In the figure above, if MNOP is a trapezoid and NOPR is a parallelogram, what is the area of triangular region MNR? GMAT Explanation
In the figure above, if MNOP is a trapezoid and NOPR is a parallelogram, what is the area of triangular region MNR?
(1) The area of NOPR is 30
(2) The area of the shaded region is 5
When I first saw this question on Exam Pack 1 I didn’t think much of it. Strangely though it comes up a ton in GMAT tutoring sessions even with students who are solid on the quant. The name of the game: stay organized, make the easy inferences, and avoid any assumptions/fake rules.
What are we looking for? The area of triangular region MNR
Table of Contents
OK – easy. You know the formula for the area of a triangle right? So start there and think about what blanks you are going need to fill in.
Anything we can add to the figure?
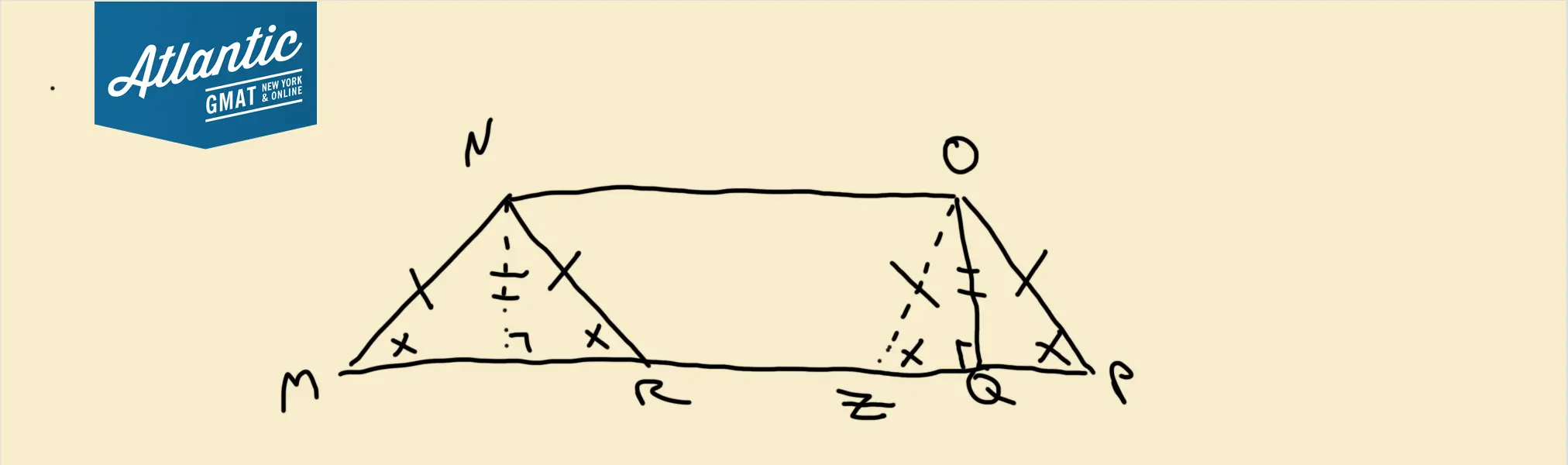
Yes! Both a parallelogram and a trapezoid have symmetry that we can use to our advantage. Also, MNR has two angles the same so the sides opposite those angles must also be the same.
If you drop an altitude at N you’ll split MNR in half (because of the two equal angles). Each of those halves is equal to the triangles QOP. You can go further and add a line at O dropping down to line MP and you’ll have two equal triangles on either side of the figure. I added all of this to the diagram below.
(1) The area of NOPR is 30
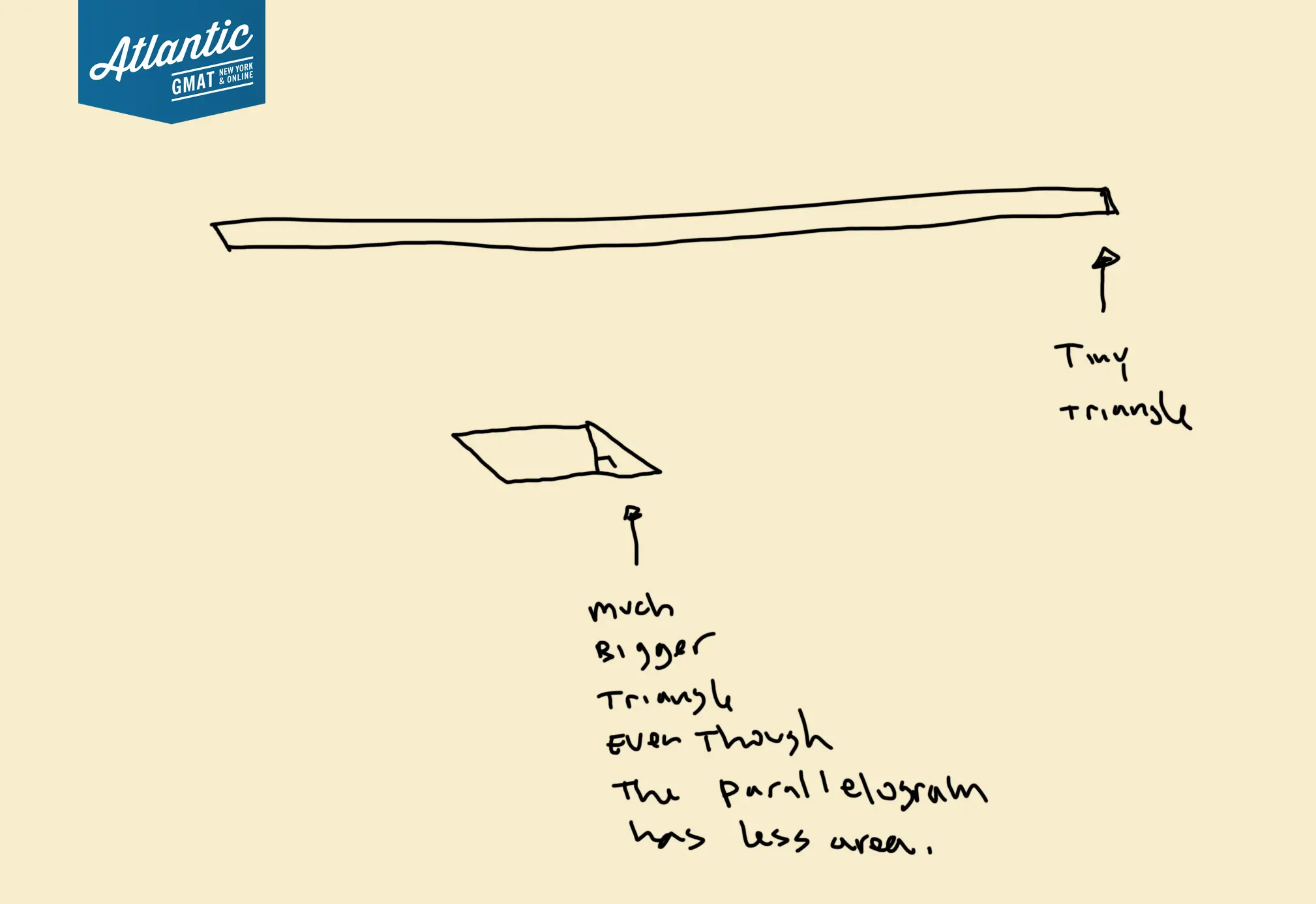
Knowing the area of parallelogram doesn’t tell us the dimensions of the parallelogram or more importantly the Base/Height of the triangle. We can make an infinite number of different parallelograms with area 30. Those variations will create different areas for the triangular regions.
You can think of this at the extremes. Let’s say parallelogram NOPR had a base of 1000 and a height of .03 (area of 30). And the parallelogram only has a very slight angle to it. The triangle will have a tiny area. You can push things in the other direction as well. Give NOPS a height of 1000 and a big angle. The triangle will have a much greater area. You can see in the diagram below that depending on the dimensions and angle of the parallelogram you can make a bigger triangle with a smaller parallelogram.
So to sum it up: just because you know the are of a parallelogram doesn’t mean you know the area of the triangles in a parallelogram.
INSUFFICIENT.
(2) The area of the shaded region is 5
If we know the area of the shaded region then we can just double that to get the area of triangular region MNR. SUFFICIENT.
Correct Answer: B
More GMAT Data Sufficiency Geometry Practice Questions!
This is from the GMAT Official Guide. It’s a tough one that has both an algebraic component and a “distortion”/testing extremes component which is similar to what we did for statement 1 above (to prove insufficiency). In the figure above, is the area of triangular region ABC equal to the area of triangular region DBA?
Here are two similar-ish DS Geometry questions from GMAT Question of the day:
GMAT Question of the Day Data Sufficiency Geometry 1
GMAT Question of the Day Data Sufficiency Geometry 2