GMAT Question of the Day – Problem Solving – Overlapping Sets (3 Group)
28 students in the senior class participate in at least one of three clubs. 24 of them are in the science club,16 are in the math club, 18 are in the history club, and 21 participate in at least two of the clubs. How many of the students participate in all three of the clubs?
A. 5
B. 7
C. 9
D. 11
E. 13
[spoiler]C.[/spoiler]
GMAT Question of the Day Solution
Of course you can tackle GMAT Overlapping Sets questions with Venn Diagrams. I never use them because I have found a lot of success with my students using these formulas which offer a more organized approach to the solution.
Here are the three formulas to memorize:
Group A + Group B + Group C + None – Doubles – 2(Triples) = Total
Singles + Doubles + Triples + None = Total
Group A + Group B + Group C = Singles + 2(Doubles) + 3(Triples)
Think about what these formulas mean. What is a single? What is a double? What is a triple? For simpler 3 group questions you may only need one of the three formulas but for more complex ones (like this one) you will use multiple equations and add/subtract them in order to isolate the variable you are solving for. Seems complicated but with a little practice it gets pretty simple. Fire away with any questions.


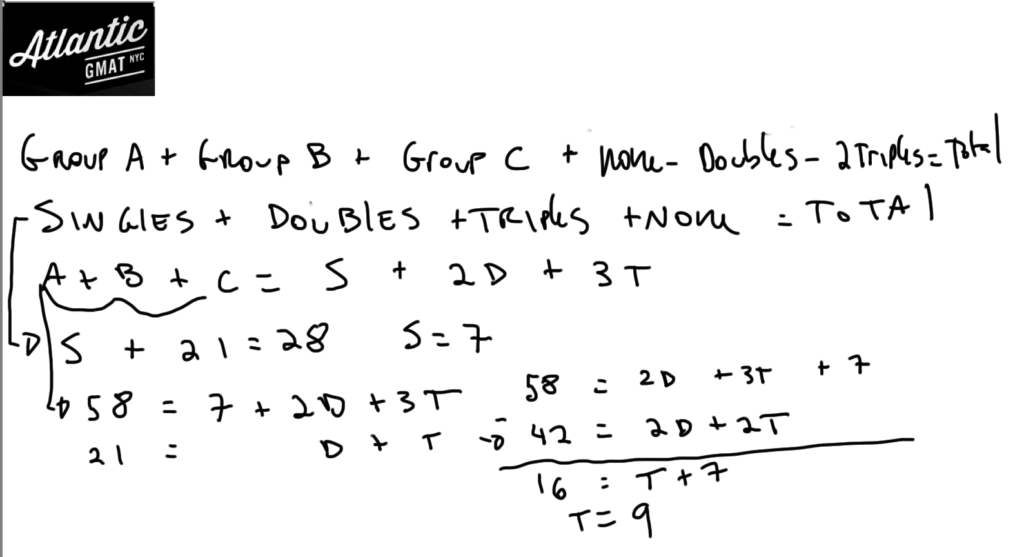
2 thoughts on “GMAT Question of the Day – PS – Overlapping Sets”
I don’t know if this is still monitored, but I’ll take a shot. I’m confused by the mechanics of this problem.
You use the second equation: Singles + Doubles + Triples + None = Total and come up with 7. I don’t understand how this is possible when we don’t know the Triples. In the work that you show, Triples just doesn’t exist. Clearly, I’m missing something. When I do it, it looks like this:
S + 21 + T + 0 = 28. So there are two variables that we do not know. How did you account for the Triples?
I hope that question makes sense. Any help is appreciated. Thanks.
S + 21 + T + 0 = 28. So there are two variables that we do not know. How did you account for the Triples?
We know
21 participate in at least two of the clubs
So that gives us the equation d + t = 21.
So S + D + T + None = 28
Substitute in d + t = 21.
s + 21 = 28
s = 7
Hope that helps!