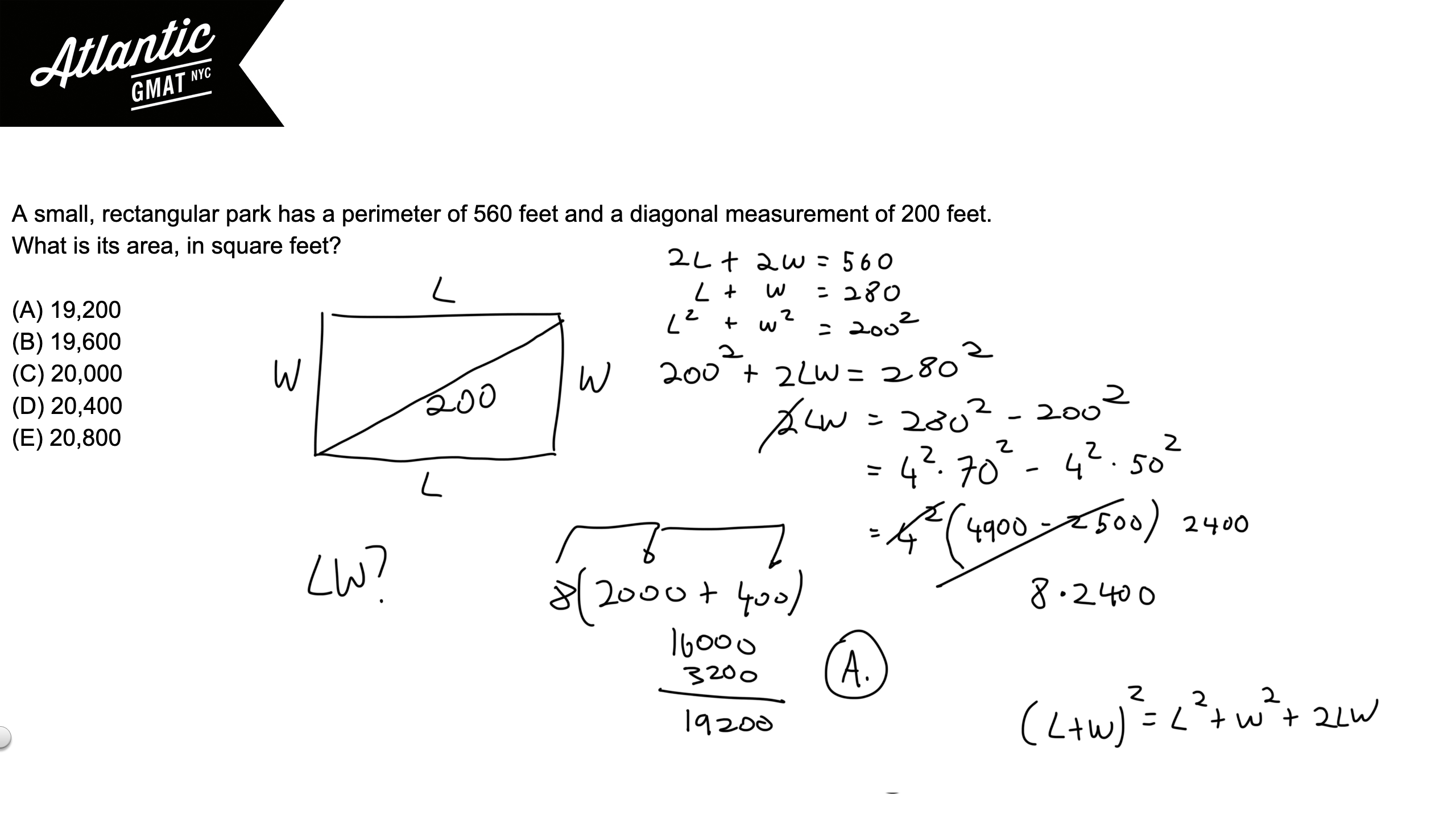
A small, rectangular park has a perimeter of 560 feet and a diagonal measurement of 200 feet. What is its area, in square feet?
(A) 19,200
(B) 19,600
(C) 20,000
(D) 20,400
(E) 20,800
This is a very basic GMAT geometry question: area of a rectangle given the perimeter and diagonal. System of equations. Again, the setup is easy peasy. It gets a bit tricky once you need to simplify to an answer. Depending on how you approach the execution you might get stuck. In addition, the answer choices are bunched closely together so you can’t really estimate/approximate.
What should you do if encountered with this type of situation on your GMAT? Panic! Just kidding. Remind yourself that there’s likely a simple way to approach things. Remember that unless a number is prime you can pull it apart. Often then there’s an easier “shape” to a number depending on what you’re trying to do.
In this case, by pulling out some factors we can:
- Do easier math with known multiples
- Divide by two
Also, with exponents often you end up factoring. So given that you have a bunch of exponents present factoring should come to mind. These simple setup/tricky execution questions aren’t uncommon so it’s important to work on being flexible in how you approach your GMAT arithmetic. Hope this is helpful. Comment with any questions!
Video Solution: A small, rectangular park has a perimeter of 560 feet and a diagonal measurement of 200 feet. What is its area, in square feet?
Additional GMAT Geometry questions with a challenging follow through
In a certain sense these questions are quite different but I think what’s challenging about them is the same. They have a bunch of algebra to get to the answer and untangling that is the point at which most people get stuck. The perimeter of a certain isosceles right triangle is 16 + 16√2. What is the length of the hypotenuse of the triangle?
Here’s another difficult geometry question from the GMAT Prep Tests 1/2 that has a similar style. The focus is on the algebra/setup not the geometry:
And finally here’s a great GMAT geometry puzzle from GMAT Question of the Day. It’s tough but I’ve seen ones just like it on test day. It has the same type of challenging algebra follow through as the park question above.