In a certain city, 80 percent of the households have cable television, and 60 percent of the households have videocassette recorders. If there are 150,000 households in the city, then the number of households that have both cable television and videocassette recorders could be any number from:

In a certain city, 80 percent of the households have cable television, and 60 percent of the households have videocassette recorders. If there are 150,000 households in the city, then the number of households that have both cable television and videocassette recorders could be any number from:

(A) 30,000 to 90,000 inclusive
(B) 30,000 to 120,000 inclusive
(C) 60,000 to 90,000 inclusive
(D) 60,000 to 120,000 inclusive
(E) 90,000 to 120,000 inclusive

Video explanation below! This is a 2 group overlapping sets question. How do I know? Well, you’ve got two categories, Cable Television and Videocassette Recorders. Households are either in cable, video, both, or neither. This sorting of people or things into two categories usually indicates a two group overlapping sets question. These are best solved using a 2 group matrix (see diagram below).

Let’s get organized!

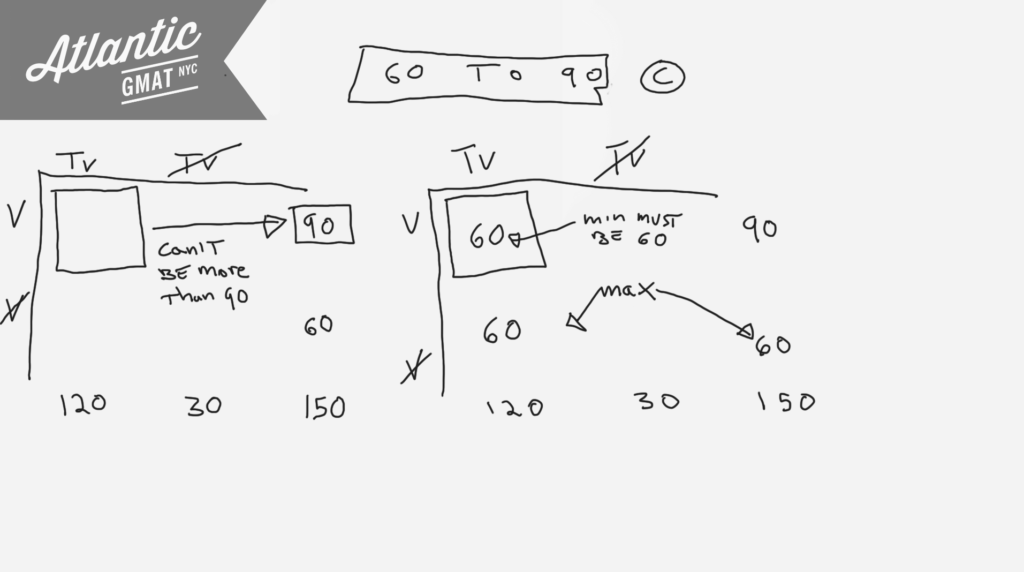
The first step is to place your actual numbers into the chart. The only one we start with is 150,000. You can safely chop off the zeros to compact a bit. Take 80% and 60% of 150 to derive total Cable Television and total Videocassette Recorders and make as many inferences as you can to fill in the chart. With numbers in place you can see that the Videocassette and Cable TV box can’t be more than 90 people because total Videocassette is 90 (if the total is 90 one of the components of the total can’t be more than 90). So the max households that have both Cable Television and Videocassette Recorders is 90. Since total Cable TV is 120, and the max Cable TV but not Videocassette is 60 the min both Cable TV and Videocassette could be is 60. So the number of households that have both cable television and videocassette recorders could be any number from 60,0000 to 90,0000. C. 

Here it is worked out:

Video Explanation For: In a certain city, 80 percent of the households have cable television, and 60 percent of the households have videocassette recorders. If there are 150,000 households in the city, then the number of households that have both cable television and videocassette recorders could be any number from:

More GMAT overlapping sets practice questions!

Here’s an overlapping sets question that adds in a bit of probability. Don’t let the probability component get in your way! Often, probability questions are easy. Take it step by step.

Among a group of 2,500 people, 35 percent invest in municipal bonds, 18 percent invest in oil stocks, and 7 percent invest in both municipal bonds and oil stocks. If 1 person is to be randomly selected from the 2,500 people, what is the probability that the person selected will be one who invests in municipal bonds but NOT in oil stocks?

Here’s one from GMAT Question of the Day that’s in the same vein. It also has percents/proportions and will give excellent practice using the two group overlapping sets matrix.

GMAT Question of the Day 2 group overlapping sets proportions and percents

This one is a bit different but will still give you 2 group practice and will give you exposure to overlapping sets on data sufficiency which often comes down to systems of questions/counting equations.

GMAT Question of the Day 2 group overlapping sets Data Sufficiency

And another challenging Data Sufficiency overlapping sets question. Again, deals with counting equations/system of questions.

GMAT Question of the Day Challenging 2 Group Overlapping Sets Data Sufficiency Counting Equations