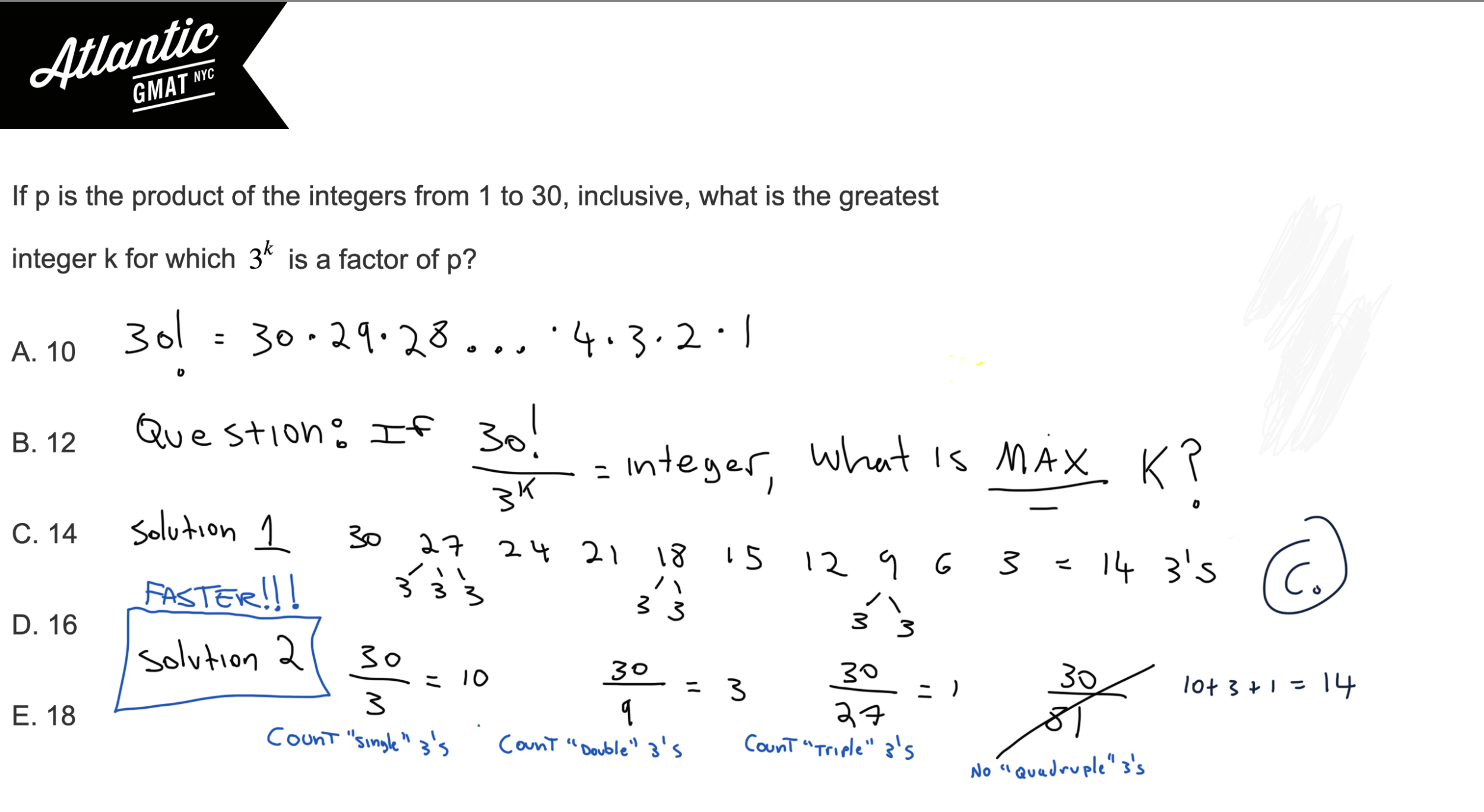If p is the product of the integers from 1 to 30

If p is the product of the integers from 1 to 30, inclusive, what is the greatest integer k for which 3^k is a factor of p? GMAT Explanation

If p is the product of the integers from 1 to 30, inclusive, what is the greatest integer k for which 3^k is a factor of p?

A. 10

B. 12

C. 14

D. 16

E. 18

Here’s a GMAT factorials puzzle from the GMAT Official Guide. I always tell GMAT tutoring students that this is a fantastic questions to get on a test, even though, at least initially, most people get it wrong. Why is it a good one? Once you know how to solve this puppy:

  1. It’s pretty easy to recognize it again
  2. It’s relatively quick to solve

Let’s break this down.

p is the product of the integers from 1 to 30. This just means 30!. What’s 30!? It’s a the product of the integers from 1 to 30. Oh. Yeah. 30*29*28*27……*3*2*1

3^k is a factor of p. This means that 30! must be divisible by 3 raised to the k power. So 30!/3^k = integer.

We want to find the GREATEST integer k. Clearly you could make k = 1 and that would work as 30!/3 is an integer. But, again, we want the greatest k. So the question boils down to, how many 3’s are in 30!?

There are two ways to do this. Let’s start with the slow but practical way.

List out the components of 30! that are divisible by 3 and then count up all of your 3’s. 30, 27, 24, 21, 18, 15, 12, 9, 6, 3. Keep in mind that 27 has 3×3’s, 18 has 2×3’s, and 9 has 2×3’s. So you end up with 14 3’s. Not bad.

Here’s the faster/cleaner way to approach these factorial questions. Take the factorial and divide it by the number you’re testing, in this case 3.

30/3 = 10. That means that there are 10 numbers from 1-30 that are divisible by 3. Done! Nope. Not yet because there are some numbers from 1-30 that have more than one 3 (see above list).

30/9 = 3. Next, up the power of 3 so that we’re dividing by 9. This tells us that there are three numbers from 1-30 that have two 3’s. Great – that was easy! Well, not quite there yet because there are numbers from 1-30 that have three 3’s.

30/27 = 1. Up the power once more so that we’re dividing by 27. That counts the number of 27’s from 1-30 or the number of numbers with three 3’s. There’s just one, 27.

30/81 = doesn’t fit. 81 doesn’t fit into 30 so that tells us that there are no numbers from 1-30 that have four 3’s. That’s where you stop.

Then just add those, 10 + 3 + 1 = 14.

The explanation for this second method is much longer BUT the method itself tends to be much quicker than the manual calculation.

if p is the product of the integers from 1 to 30, inclusive, what is the greatest integer k for which 3k is a factor of p? gmat explanation diagram

Video Solution: If p is the product of the integers from 1 to 30, inclusive, what is the greatest integer k for which 3^k is a factor of p?

Additional GMAT Factorial Puzzle Practice Questions

Not the same factorial setup but a solid GMAT Question of the Day puzzle example to get you thinking in a GMAT kind of way

Here’s another GMAT Question of the Day to sharpen your GMAT puzzle skills.

And a very challenging question of the day exponents puzzle

Lastly, a challenging GMAT q of the day divisibility/exponents puzzle