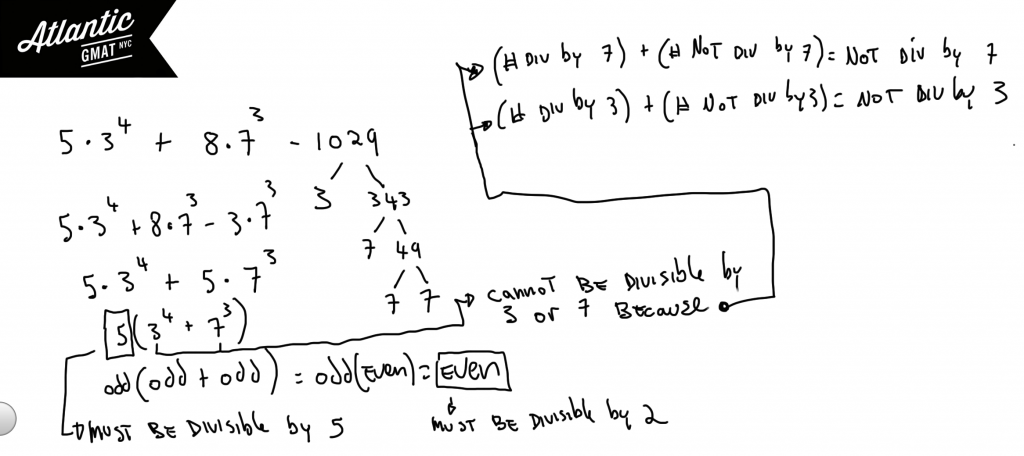GMAT Question of the Day – Problem Solving – Exponents/Number Properties
If K is a factor of 3^4 + 3^4 + 3^4 + 3^4 + 3^4 + 7^3 + 7^3 + 7^3 + 7^3 + 7^3 + 7^3 + 7^3 + 7^3 – 1029 then which of the following are possible values of K?
I. 2
II. 5
III. 7
A. I only
B. II only
C. III only
D. I and II only
E. II and III only
[spoiler]D.[/spoiler]
GMAT Question of the Day Solution
Number Properties Problem Solving questions are rarer than Data Sufficiency number properties questions but still do pop up every once in a while. This GMAT question of the day combines number properties/divisibility and exponents. Again, the key is organization. Apply your basic exponents rules. Round up your like terms. Factor. Analyze.
Step one should be to gather all of your 3’s and 7’s. Step two should be to prime factor 1029 with the assumption that 1029 will reveal 3’s and 7’s. You can see that 1029 has three as a factor because 1 + 2 + 9 = 12. 12 is visible by 3 so 1029 is as well. Now combine everything. Notice that there is a 5 attached to each term. Factor that out. 5(3^4 + 7^3) must be divisible by 5. It also must even and so divisible by 2. Why even? Because odd + odd = even. This expression cannot be divisible by 3 or 7 because (divisible by x) + (not divisible by x) must equal a number that is NOT divisible by x. This rule is very helpful, especially on GMAT Data Sufficiency questions.