If n = (33)^43 + (43)^33 what is the units digit of n? GMAT Explanation, Video Solution, and More Practice!
If n = (33)^43 + (43)^33 what is the units digit of n?
A. 0
B. 2
C. 4
D. 6
E. 8
Units digits questions always come up in tutoring. They’re great because they’re very formulaic (unlike a lot of the GMAT). I remember really struggling for time on an official GMAT I was taking and then question 31 was: What’s the units digit of 8^52? Blasted through that one is 20 seconds and: 770! I was psyched! Anyways, rest assured that GMAT units digits questions are easy.
Every units digit has a multiplication pattern with the longest patterns being only 4 variations long. So let’s look at some units digit patterns and then we’ll apply what we learn to the question at hand. With each of these we’re just raising the power to get to the next number in the pattern:
1: Always ends in 1
2: 2, 4, 8, 6 (2^1, 2^2, 2^3, 2^4). Then you can see that 2^5 goes back to “2”.
3: 3, 9, 7, 1
4: 4, 6
5: Always ends in 5
6: Always ends in 6
7: 7, 9, 3, 1
8: 8, 4, 2, 6
9: 9, 1
0: Always ends in 0
You don’t have to memorize these! They are easy enough to derive in the moment. An important note when creating units digit patterns: you don’t have to multiply the entire number to yield the units. You just need to multiply the units digits. So 37*37, no need to multiple the whole thing. Just take 7*7 and you know that number ends in 9.
Ok, easy right? Let’s get back to: If n = (33)^43 + (43)^33 what is the units digit of n?
Let’s figure out the units for each one and then, guess what, you just add those units digits. Adding and subtracting units digits is also do-able without having to deal with the entire number.
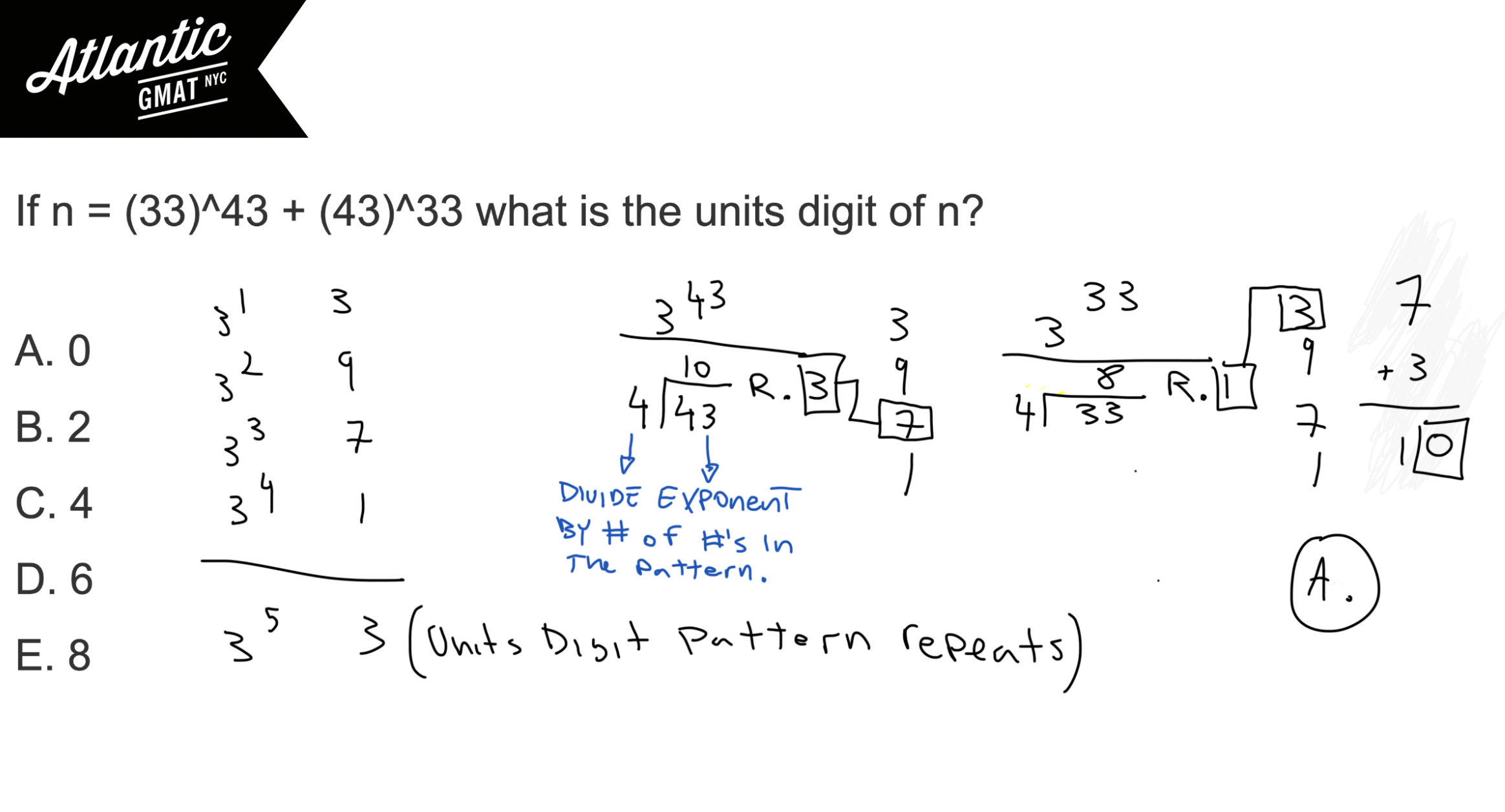
You might be wondering how we’re going to get to the 43rd number in the pattern for (33)^43. Well, that’s just a question of divisibility. The units is 3 so we have a pattern of 4 numbers. How many 4’s fit into 43? 10 with 3 leftover. The leftover is the important part.
3
9
7
1
That 3 means we end in 7. There are 40 complete patterns of 4 and then 3, 9, 7 gets you to 43. Put another way, 7 is the 43rd number in the pattern.
Same thing for 33. There are 32 complete patterns of 4 with 1 leftover. So that leaves a units digit of 3.
You can test this all out by just writing out 3, 9, 7, 1 a bunch and counting to the 33rd and 43rd terms. You will find 1 and 7 respectively. But again, easy way to figure out where you are is to divide the exponent by the number of numbers in the pattern.
Then just add the units to yield the units of the sum of the numbers: 7 + 3 = 10. So the units digit of n is 0.
Correct Answer: A
Video Solution: If n = (33)^43 + (43)^33 what is the units digit of n?
Additional GMAT Units Digit Practice Questions
Here is a very similar units digit question from GMAT Question of the Day but it has an important twist. Make sure you follow through with all of you basic math rules.
This GMAT question of the day puzzle goes beyond digits into powers of 10 but is a great one to be familiar with as I’ve seen this style on a multiple official GMATs.
Here’s a digits Data Sufficiency Question from GMAT Question of the Day It’s a bit more involved but good practice.