GMAT Question of the Day – Problem Solving – Probability
Katie has a bag of marbles which contains 3 blue marbles, 3 red marbles, and 2 yellow marbles. If she arranges her marbles in a line what is the probability that the marbles will be grouped by color?
A. 3/280
B. 3/560
C. 5/632
D. 7/632
E. 7/635
[spoiler]A.[/spoiler]
GMAT Question of the Day Solution
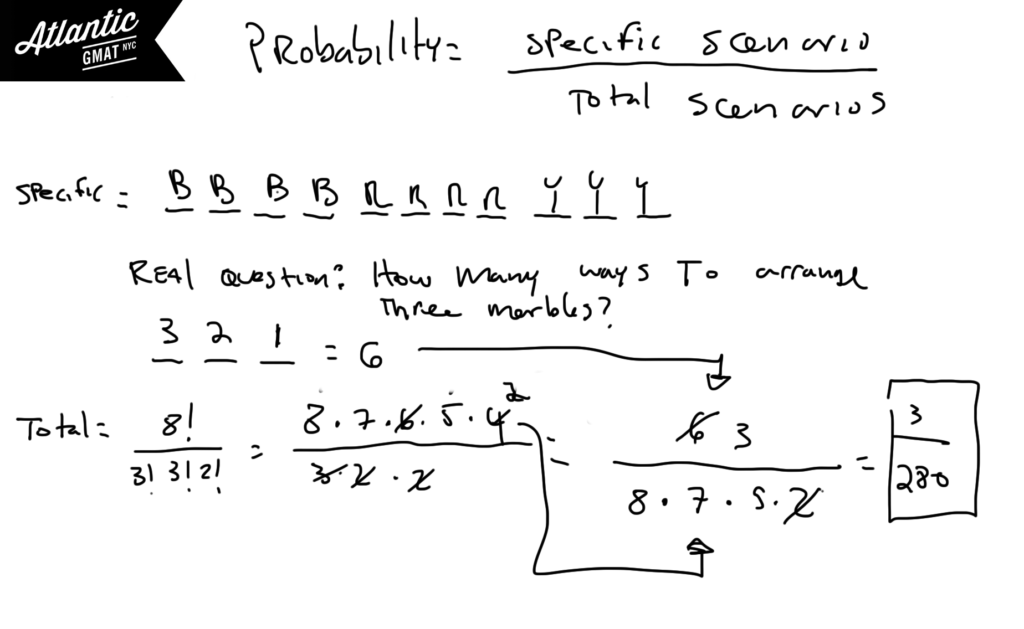
GMAT probability can feel very easy or near impossible depending on your mastery of a few simple rules. Probability breaks down to:
Specific Scenario (in this case the marbles arranged by color)/Total Scenarios (in this case the total ways the marbles can arranged). It’s important to realize that when calculating the total ways that the marbles can be arranged that switching two red marbles does not make a new arrangement (or switching two greens or switching two yellows). We need to use the non-unique ordering formula. The factorial of the total items (in this case 8 marbles so 8!) divided by the factorial of each individual item (3!, 3!, 2!). Any time that you are arranging/ordering non-unique items you need to use this formula.
Also realize that with the specific scenario the real question is: how many ways can you arrange three different colored marbles? Why? Well, you have to group each color so really each group just represents a color. Arranging three unique things is just 3!
Quick note on arithmetic. Notice in the solution that I didn’t multiply 8, 7, 5, and 2 but waited until the very end so that I could simplify more. On the GMAT it’s helpful to wait on multiplication until you are sure that you won’t be able to simplify further. The GMAT usually gives you a way to keep your arithmetic manageable. Get in the habit of picking up on these cues.
More GMAT probability and combinatorics examples
Here’s another challenging GMAT probability question that’s similar but different to the one above. I like it because it reinforces staying practical with your solutions. Not everything needs a formula. Here it is: Tanya prepared 4 different letters to be sent to 4 different addresses.