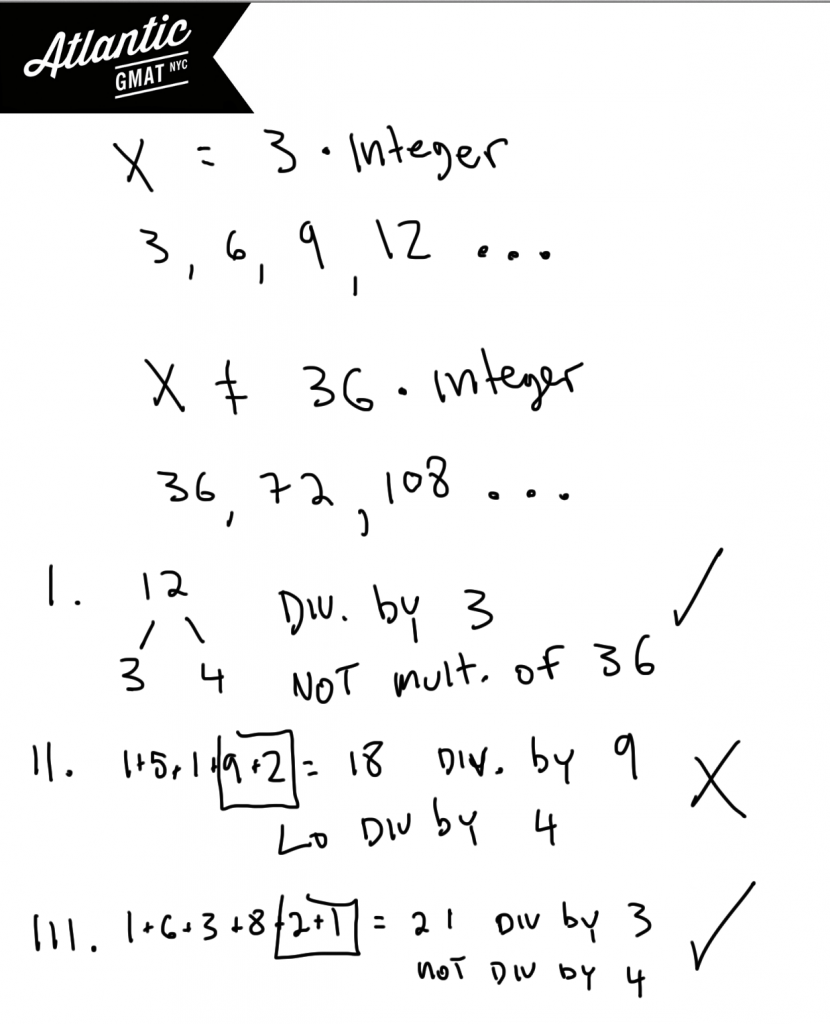GMAT Question of the Day – PS – Number Properties 5

GMAT Question of the Day

GMAT Question of the Day – Problem Solving – Number Properties/Divisibility

If x is a positive multiple of 3 but not divisible by 36 then which of the following values could be a factor of x?

I. 12

II. 15192

III. 163821

A. I Only

B. II Only

C. III Only

D. I and III Only

E. I, II, and III

[spoiler]D.[/spoiler]

GMAT Question of the Day Solution

I spend a lot time in GMAT tutoring sessions teaching how to recognize GMAT question types. By recognizing the question you can apply the right tools to get to the answer. When GMAT questions have such keywords as divisible by, multiple of, and factor of you should be thinking about divisibility and prime factors.  In this question of the day we have a few of these words and so should be considering the prime factors (or the very least the factors) of these numbers. We know that x is a positive multiple of 3 so that x could be 3, 6, 9… We also know that x is not a multiple of 36. So that x cannot have 9 and 4 as factors. In this case we don’t need to worry about the complete prime factorization because it’s easy enough to see what is happening. That means that x can be any multiple of 3 that is not divisible by both 9 and 4. Another way to say that is that x can’t be a number with two 2’s and 3’s. x can have to two 2’s but not two 3’s or two 3’s but not two 2’s. We just can’t have both of those numbers together because then the number will be divisible by 36 – a situation that is out of bounds in this question.

In the answer choices you need to eliminate answers that are either

1. Not divisible by 3

2. Divisible by both 4 and 9 (divisible by 36)

In this question and in many others you will be helped by knowing some basic divisibility rules. Any number whose digits add to 3 are divisibly by 3. Any number whose digits add to 9 is divisible by 9. If the last two digits of a number form a number that is divisible by 4 then the entire number is divisible by 4. You can use these rules to eliminate choice II. It is divisibly by both 9 and 4. Choices I and III both follow our rules.

gmat question of the day problem solving number properties divisibility solution diagram

Additional GMAT Divisibility and Remainder Practice Questions

Here’s a difficult divisibility/remainder question from the GMAT Official Guide. It’s a bit different in terms of specific content but allows you to practice a practical approach to number properties.

And here’s a nice remainder skill builder question from GMAT Question of the Day that will teach you a couple of strategies you need for the GMAT Official Guide question.