GMAT Question of the Day – Problem Solving – Geometry/Puzzle
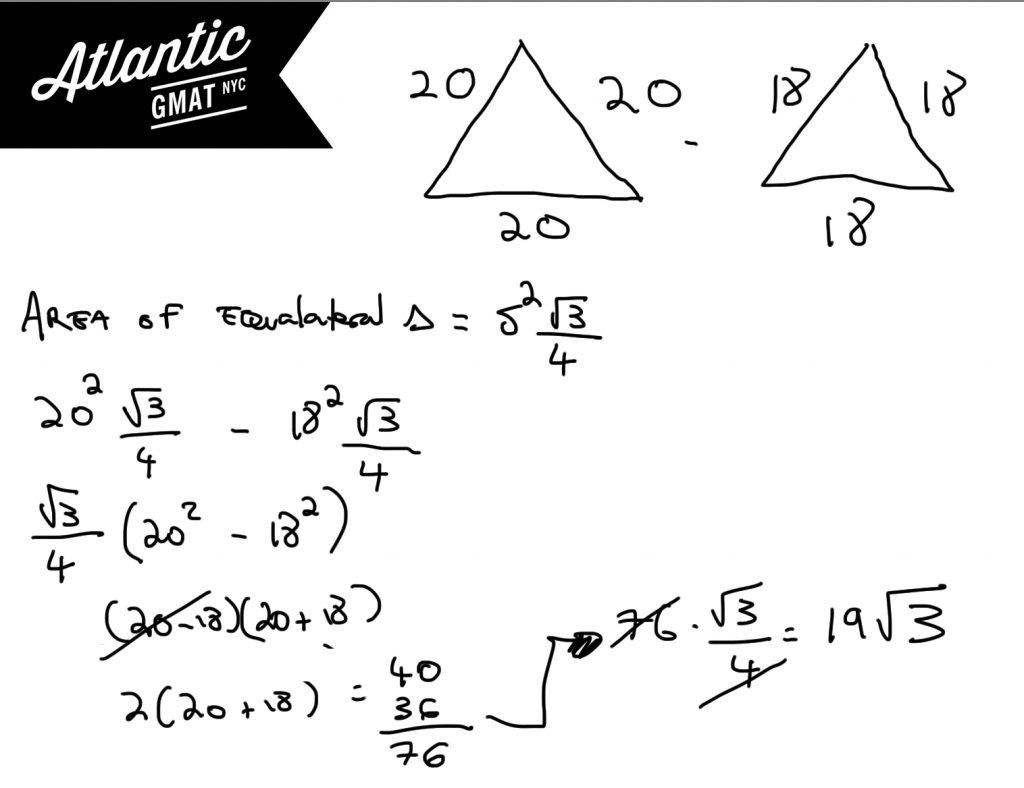
The measurements obtained for the sides of a certain triangle are 18 centimeters by 18 centimeters by 18 centimeters. If each of the sides has a measurement error of at most 2 centimeters, which of the following is equal to the maximum possible difference between the actual area of the triangle and the area calculated using these measurements?
A. 17√3
B. (35/2)√3
C. 18√3
D. (39/2)√3
E. 19√3
[spoiler]E.[/spoiler]
GMAT Question of the Day Solution
Although this GMAT question involves geometry it is also a bit of a puzzle because of the measurement error portion. If you’re not sure how the measurement error will affect the area you might want to try some small numbers to get a feel for the question. Try a triangle with sides measuring one versus a triangle with sides measuring three. Let’s remember that we want the maximum difference so you should make the measurement error a plus not a minus. Why a plus? Because the bigger the numbers the more the difference of two will make. The difference between 1000*1000 and 1002*10002 is much greater than the difference between 3*3 and 5*5. So we want the numbers to be as big as possible.
The other thing that will help in this question of the day is: the formula for the area of an equilateral triangle. For my GMAT tutoring students I try to keep the esoteric formulas to a minimum (no memorizing standard deviation here!) but this formula is useful. Side^2 * (√3/4)
Once you set up the expression you should notice that you can factor out √3/4. Once you’ve done that you’ll see a difference of squares. Go for it! Using this special quadratic will make the simplifying easier.
More Challenging GMAT Geometry Examples
Here’s a tough one from the GMAT Prep Tests 1 and 2. The focus is on the setup and then the algebra not the geometry. The geometry portion boils down to: the area of a square and the area of a circle.
Here’s a tough GMAT geometry question that’s similar but different. I find it similar because like the “measurement error” question above it focuses a bit more on the algebra than the geometry.
Same deal with this one. The geometry aspect is very simple. You don’t need to make a lot of inferences. The challenge is in the algebra.