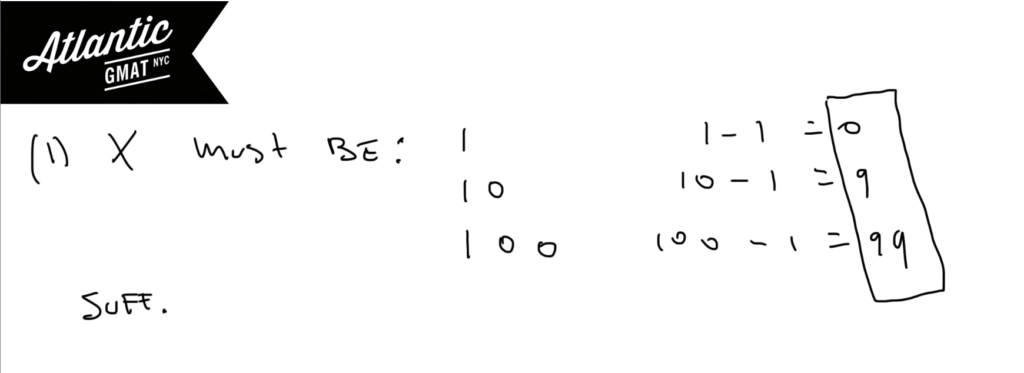GMAT Question of the Day – Data Sufficiency – Number Properties/Divisibility

If x and y are both positive integers is (x^y – 22)/3 equal to an integer?

(1) The sum of the digits of x is equal to 1

(2) y > 1

[spoiler]A.[/spoiler]

GMAT Question of the Day Solution

This question of the day deals with divisibility. Usually with this type of question it will help to make some kind of list or chart to see if there is some kind of pattern. Some GMAT tutoring students are resistant to making charts and lists on Data Sufficiency questions because this type of work hasn’t paid off for them in the past. However, you have get a feeling for the types of questions that require making charts, lists, and writing out scenarios. There are plenty of times when these tools will make a DS question much simpler.

For this question you ought to think about the fact that every third number is divisible by 3. So 1, 2, 3 or 2, 3, 4, or 3, 4, 5. Those are all the different patterns for three. Notice that the number divisible by three can be in either of the three places as can the number that is 1 away from being divisible by 3 and the number that is 2 away from being divisible by 3. Notice that in terms of divisibility by 3, 1 is the same as 4; 2 is the same as 5. So there is a pattern. If we can figure out where x is in the pattern we’ll be able to decide whether subtracting 1 will yield a number divisible by three.

(1) This tells us that x is either 1, 10, 100… That means that x will always be a number that is 1 away from divisible by 3. Therefore x-1 will always be divisible by three. You can also understand this with divisibility rules. If the sum of the digits equals a number that is divisible by three then the number itself is divisible by three. So if you know the sum of the digits of a number then you know what you can add/subtract to make that number divisible by 3. The same strategy will work for 9. Sufficient.

(2) The value of y makes no difference provided that y is a positive integer. Larger values of y just add more zeroes after the one. That will not change the divisibility by 3. If y could have been negative then we would have had to consider its value because a negative y would have created a fraction. Insufficient.

More GMAT Data Sufficiency Divisibility Practice Questions

Here’s one more  GMAT Data Sufficiency Divisibility question with in depth explanation from the GMAT Official Guide