GMAT Question of the Day – Data Sufficiency – Combinatorics
A team is composed of exactly 4 executives and 3 associates. How many such teams can be formed?
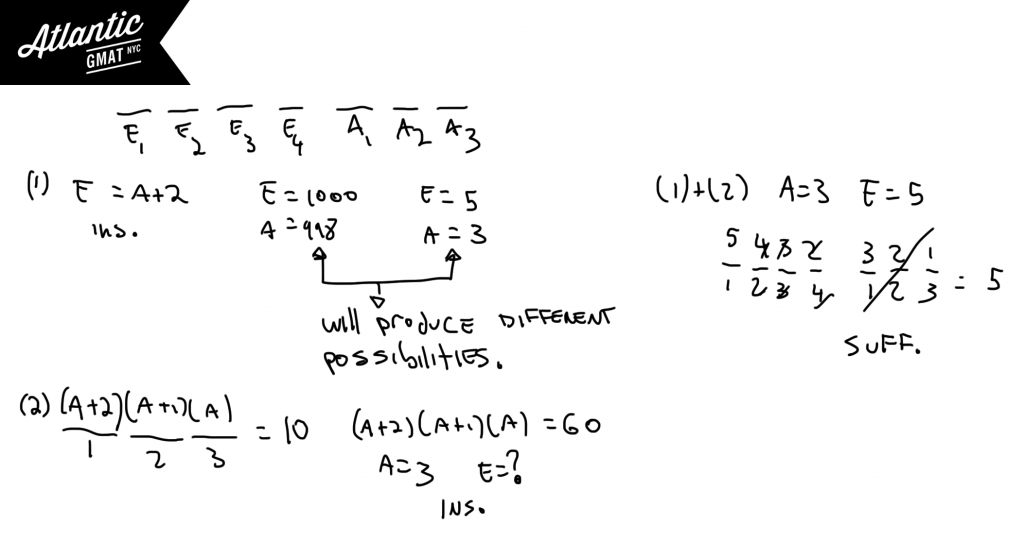
(1) If two fewer executives were available for selection there would be equal an number of executives and associates available for selection.
(2) If two more associated were available for selection exactly 10 different teams of 3 associates could be selected.
[spoiler]C.[/spoiler]
GMAT Question of the Day Solution
GMAT combinatorics questions do not have to be difficult. They seem challenging because they are opaque. It’s not always easy to see through them. Often though, there is very little that you need to do in order to get the answer. As with the rest of the GMAT it’s all about getting the right context. Categorizing the question. Are you putting together a team or creating an order? If it is an order is it unique? How many “players” do you have? How many slots on the team do you have for these players? In this GMAT question of the day we have 7 slots which are separated into executive slots and associate slots. We’re not given the number of executives/associates. We’ll need to figure that out with the statements (if possible).
Statement 1 tells us that that executives = associates + 2 but does not tell us anything about the real numbers. So there could be 998 associates and 1000 executives or 5 associates and 7 executives. Those two sets of values would produce different numbers of teams. Insufficient.
Statement 2 tells us that we have 3 associates but we have no information on the executives.
Putting the together we have the number of people in each group and can calculate the number of teams. Hurray.