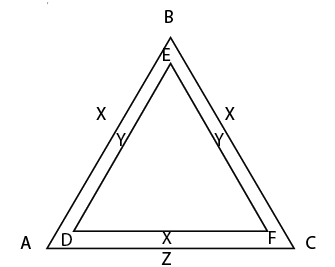
GMAT Question of the Day – Problem Solving – Geometry

If DF || AC and x = 1.5y, what is the ratio of the areas of triangle ABC and triangle DEF?

A. 4/7

B. 3/2

C. 7/4

D. 9/4

E. 16/3

[spoiler]D.[/spoiler]

GMAT Question of the Day Solution

The rules governing similar triangles are relatively basic. So what’s challenging about GMAT similar triangles questions?

1. Spotting that the question is in fact testing similar triangles

2. Organizing the information so that it is clear which angles and sides are corresponding.

How can you make GMAT similar triangles questions easier? First thing, whenever you see triangles that share sides or triangles within triangles consider that the triangles may be similar. Remember that you only need two angles to be the same in order to prove similarity. One thing that can help to keep things organized is to label the angles. You don’t need to know that actual values. Just giving the angles variables will help illustrate which angles are in fact the same and which sides correspond with one another.

In this case the two triangles must be similar because two of the angles are the same. You can infer this information by the fact that DF and AC are parallel (parallel lines cut by a transversal). Now you can substitute x for y and find the ratio of the sides. Here’s a GMAT shortcut: the square of the ratio of sides is equal to the ratio of the areas.