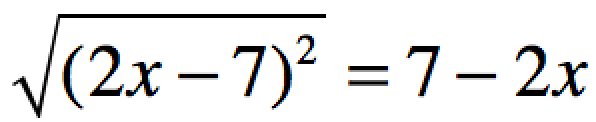GMAT Question of the Day – Problem Solving – Absolute Value

If 2x – 7 is not equal to zero, which of the following must be true:

I. x < 7/2

II. (2x)^2 < 49

III. |x| * x < 0

A. I

B. II

C. I and II

D. II and III

E. I, II, and III

[spoiler]A.[/spoiler]

GMAT Question of the Day Solution

Whenever dealing with GMAT absolute value questions always consider the signs. Also think about this: |x| = √x^2  These two expressions are equivalent. Switching from one format to the other can be helpful. It’s a bit like factoring with difference of squares. It doesn’t always help but it is worth doing so that you can see if the factoring reveals an inference. In GMAT tutoring I like to point out that GMAT questions should be looked at as little games. Approach them as games. Be curious. Try things out. Especially in your practice.

In this GMAT question of the day it will help to switch to the absolute value format. Knowing that the left side is an absolute value guarantees that it will not be negative. And since it cannot be zero (given in the question) it must be positive. That means that right side of the equation must also be positive. Set up that inequality and solve for x. x must be less than 7/2. The first roman numeral must be true. The second is tricky because you might think it provides similar information to the first roman numeral. But because the expression is squared we can also consider negative values for x. x could be -10 so the second roman numeral isn’t always true. The third roman numeral simplifies to x < 0. This is not always true as x can be any number less than 7/2.