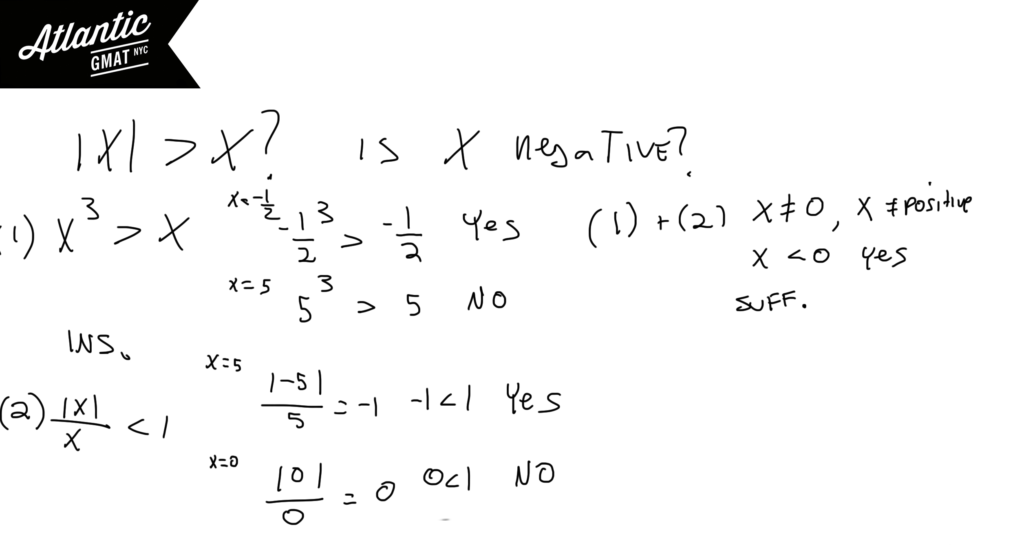GMAT Question of the Day – Data Sufficiency – Absolute Value/Number Properties

Is |x| > x?

(1) $$x^3$$ > x

(2) $$\dfrac{|x|}{x} < 1$$

[spoiler]C.[/spoiler]

GMAT Question of the Day Solution

Continuing on with more GMAT absolute value questions. These can make your head spin if you’re not organized. When dealing with absolute value consider two things:

1. Absolute value is the distance from zero and hence is always positive.

2. GMAT absolute value questions tend to focus on positive/negative or the signs of the underlying number (because absolute value hides the sign)

Let’s consider a few important cases that will help with GMAT absolute value questions.

1. If x < 0 then |x| > x. This makes sense because the absolute value will always be positive.

2. If x < 0 |x|/x will be less than 0. Again, if x is negative you will have a positive over a negative leaving a negative number.

3. If x is a negative fraction then |x|/x is less than x because the fraction will equal -1 (more negative is a smaller number).

4. |x| = √x^2 (just memorize this as it can be helpful).

Statement (1) This tells us that x is either a positive number or a negative fraction but the former produces a no and the latter produces a yes so this statement is insufficient.

Statement (2) This tells us that x must negative or 0. Again, a negative value produces a yes while zero would produce a no. Insufficient.

Statement (1) and (2) Together we can eliminate the zero option (statement 1) and the positive option (statement 2) so x must be negative. If x is negative then |x| > x. So the answer is yes. The statements together are sufficient.