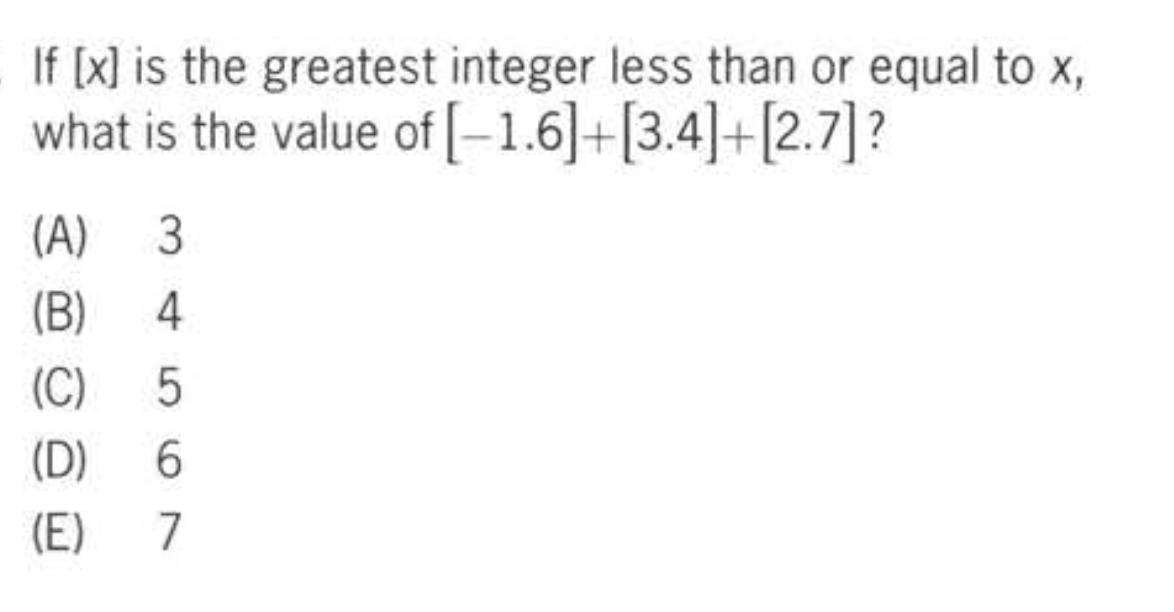GMAT Functions Explained (with worked through example questions)
You guessed it, we’re going to dive into GMAT functions, a quant question type that comes up on just about every GMAT. Good news: there’s nothing inherently difficult about GMAT functions. Bad news: GMAT students tend to get hung up on them. Why? Often GMAT function questions look strange or have a dense set of instructions that can distract from the basic premise of the questions. We’re going to break down what a function is and then work through some GMAT examples so, hopefully, by then end of this article you’ll feel confident on the majority of GMAT function questions.
What is a function?
What is a function? A rule that defines a relationship between one variable and another. That’s it. So function questions relate one variable to another. Figuring out that relationship and applying it is the key to success. There are two main types of GMAT functions. Ones with symbols that represent a set of instructions that you need to apply and ones using f(x) to define an equation (or sometimes also a set of instructions) that you apply to whatever is in the parentheses (where x is). Let’s look at an example of a symbol function from the GMAT Official Guide:
GMAT Functions: Symbol Questions
For symbol questions take your time reading. Really slow down. It’s not unlikely that you’ll start off feeling a little confused. That’s OK. It’s fine if it takes a second to understand the system. And that’s true for all GMAT questions. Don’t feel pressured to understand everything right away. Let the inferences develop.
For this function, the circle indicates that the product of the two variables needs to be placed under a square root. So whatever numbers replace the variables X and Y need to do the same thing. It’s not uncommon to have a nested function or a function within a function so that you need to apply the rule multiple times. Not a problem. Start from the innermost parenthesis and work out. Again, take your time.
In this case do the 5 and 45 first and then take that result and put it through the function again with 60 as the second number. Zip, Zap, Zop and you’re done!
√(5)(45)
Let’s go ahead and factor these so we can pull out any perfect squares.
5*3*3*5
So we have two 3’s and two 5’s (9 and 25). They’re both perfect squares. We can get rid of the root and we’re just left with 15 (3*5).
Now apply the function again and we’ve got √(15)(60). Let’s factor to find perfect squares.
3*5*3*2*2*5. We can partner up the numbers, 2*2*3*3*5*5. Three sets of perfect squares (4, 9, 25). So we can get rid of the root and we’re left with 2*3*5 or 30. A.
Once again, GMAT functions are just a set of rules either given as a set of instructions represented by a symbol or as defined in an equation with f(x). Here’s one with the f(x) format:
GMAT Functions: f(x)/Equation Questions
Instead of f(x) we have f(m). Same thing. You could have f(h) or f(d) or any variable. Let’s figure out the function or instructions. It’s basically a factorial but with only the even numbers. So f(4) would be 2*4. f(6) would be 2*4*6. And so on. It’s often a great strategy to give yourself a few simple examples of the function before tackling the question itself.
So now we need f(24), 2*4*6*8*10*12*14*16*18*20*22*24. And we need to determine the greatest prime factor (GCF). There are two ways to do this:
- Work from the answers
- Work from the function
I think it’s probably a bit faster to work from the answers. Since we’re looking for the GCF start with the largest number.
(A) 23 doesn’t fit into any of our numbers or put another way isn’t a factor of f(24).
(B) 19 Same thing.
(C) 17 Same thing.
(D) 13 Same thing.
(E) 11*2 is 22 so that’s in there. Must be E.
If working form the numbers, again, start with the largest and find the primes.
24 only has 2’s and 3’s.
22 is 11*2 so that looks good. No positive even number less than 22 can have 11 or any prime greater than 11 as a factor. In order to be even a number must have 2 as a factor. So 2*11 is the least EVEN number with 11 as a factor. So 11 is the GCF of f(24).
Here’s another “f(x)” type function but this one has an equation instead of a set of instructions.
This question takes things in a slightly different direction in that we’re told the outcome but not the “x” value. We need to solve for the “x”. All you have to do is set the equation 2^x – 3 equal to 31 and solve. We don’t need the exact number just a range.
2^x = 34
Now list out the powers of two and find the range. Looks like 34 is between 2^5 (32) and 2^6 (64). E.
2, 4, 8, 16, 32, 64
Hopefully GMAT functions are feeling more approachable. Just remember (broken record alert): functions are just a set of instructions. So, read carefully and focus on getting those instructions defined. Again, it can be helpful in some cases to give yourself simple examples of what the function does before approaching the main question. If you feel a bit lost after the first read: that’s OK! That doesn’t mean that the question is difficult or that you won’t solve it correctly. It’s totally normal to not know everything right away. Part of being a GMAT master is building the confidence to stick with a question. To give yourself the space the succeed. And, remember, if things get heavy: skip! No single question is worth it.
OK, let’s explore more examples of GMAT functions!
Here’s a symbol question. Let’s go ahead and figure out the instructions: greatest integer less than or equal to x. I’ve seen several examples of this very specific GMAT function question on actual GMATs I’ve taken. This is a great candidate for giving yourself examples before answering the questions just to make sure you’ve got your head wrapped around the function.
What happens if the number is an integer, say 5? It stay at 5.(greatest integer less than or EQUAL)
What happens if the number is a positive non-integer, say 1.5? It goes down to 1. (greatest integer less than or EQUAL)
What happens if the number is a negative non-integer, say -1.5? If goes down to -2. (greatest integer less than or EQUAL. The negative numbers make things a little tricker because though -2 is smaller is has a greater magnitude).
OK, now let’s approach the question.
-1.6 becomes -2
3.4 becomes 3
2.7 becomes 2
-2 + 3 + 2 = 3.
A.
If you’d like more GMAT function examples you can take a look at these three posts. They each go into depth on a challenging GMAT function question:
For which of the following functions is f(a+b) = f(b) + f(a) for all positive numbers a and b?
For which of the following functions f is f(x) = f(1-x) for all x?
Hope that is helpful. Follow up with any comments or questions. Happy studies!