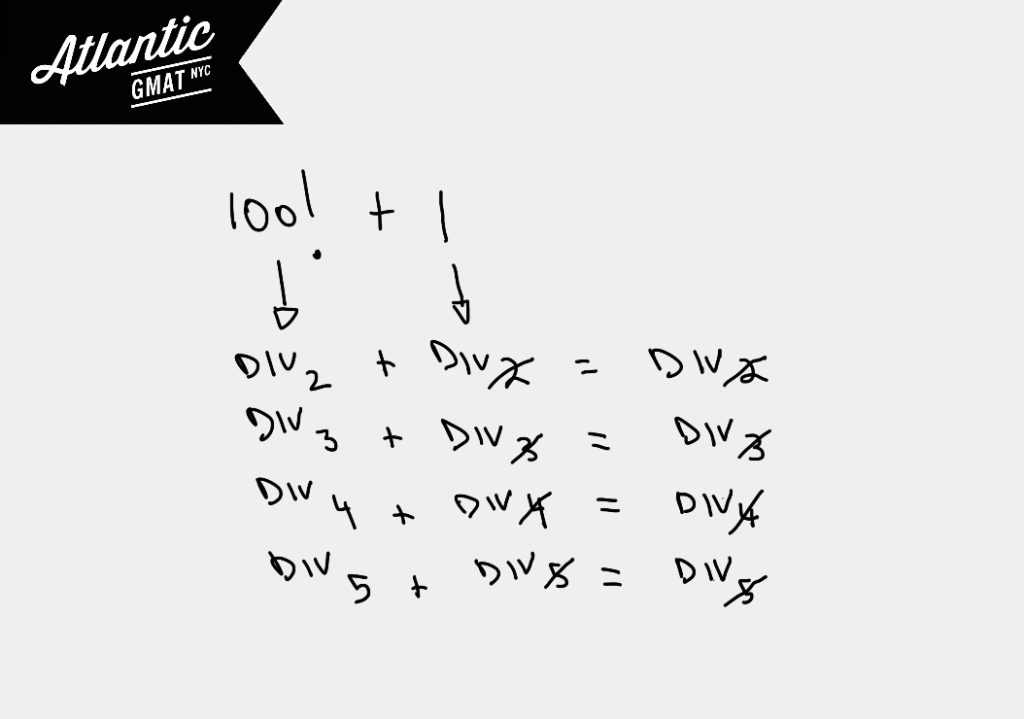For every positive even integer n, the function h(n) is defined to be the product of all the even integers from 2 to n, inclusive. If p is the smallest prime factor of h(100) +1, then p is? GMAT Explanation, Video Solution, and Additional Practice!
Table of Contents
For every positive even integer n, the function h(n) is defined to be the product of all the even integers from 2 to n, inclusive. If p is the smallest prime factor of h(100) +1, then p is?
A. Between 2 and 10
B. Between 10 and 20
C. Between 20 and 30
D. Between 30 and 40
E. Greater than 40
This is an extremely challenging GMAT question which most people will struggle to solve. If you want to start more basic here is our main page for GMAT functions with a bunch of simpler examples.
What did I do the first time I saw it: Skip! Yep, I didn’t have a good plan for it so I moved on. Here’s an article on GMAT Timing to shed some light on how to manage that precious resource.
After I reviewed this GMAT functions puzzle I noticed that the solution really didn’t require much heavy lifting and was based on:
A very simple divisibility rule which every GMAT hopeful should know!
If a number is divisible by some number and you add another another number that’s also divisible, the sum of those two numbers will remain divisible. 7 + 14 = 21. (both div. by 7 and 21 div. by 7)
If that second number is NOT divisible then the sum is NOT divisible. 7 + 15 = 22 (15 not div. by 7 so 22 isn’t either)
If neither number is divisible by a certain number then the outcome isn’t predictable. Sometimes the sum will be divisible sometimes not. 6 + 1 = 7 (neither div. by 7 but the sum is div.). 6 + 2 = (neither div. by 7 but the sum is NOT div.).
Here’s a diagram with more examples:
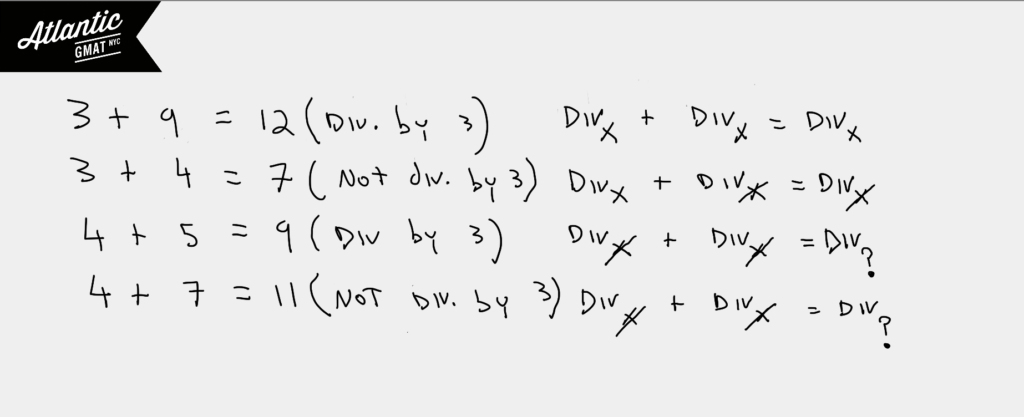
Ring a bell? Great, why don’t you try the question again before reading the rest of this explanation! Back with us? OK. Let’s break down this beast!
For every positive even integer n, the function h(n) is defined to be the product of all the even integers from 2 to n, inclusive.
The product of a consecutive set of integers should get you thinking about: factorials. What’s a factorial? You should know that! 5! or 5 factorial is 5*4*3*2*1. 3! is 3*2*1. Got it?
In this case though we’re only concerned with the even parts of the set (2 x 4 x 6 x 8 x 10…). So it’s the factorial but not including the odd numbers.
If p is the smallest prime factor of h(100) +1, then p is?
Now we know that the end of the factorial is 100. So P is the product of the even integers from 2 to 100. How should we get going?
Sometimes you just need to start arranging the information in a reasonable way (even if you don’t know where that will lead)
In this case start writing out the positive even integers from 2 to n (In our case n = 100) in order to get a sense for the numbers. Why start from 2?
Well, it’s the smallest one. It usually helps to start at the edges of a set. Do you need to write out all of the even numbers from 2 to 100? Probably not.
Again, focus on the edges say from 2 to 10 and then from 90 to 100. This idea can be applied all over the GMAT.
That doesn’t mean that the middle of a set never matters. It’s just that it tends to be that the edges provide more information and are the better place to get started.
If you have a good reason for attacking the middle of a set. Great – go for it!

Now we’ve listed out the beginning and the end of the set as defined by the function.
Let’s notice that our set consists of the positive multiples of 2 from 2 to 100 (2, 4, 6, 8, 10…).
Let’s combine this idea with the divisibility rule above. We know that our number 100! is divisible by 2. 100! + 1 is not divisible by 2.
Why? Well, 100! is divisible by 2. 1 is not divisible by 2. So Div by 2 + Not Div by 2 = Not Div by 2.
That also means 100! + 1 isn’t divisible by 3, 4, 5, 6…up through at least 50 because 100! is divisible by those numbers while 1 isn’t divisible by any of them.
So the smallest number that 100! could be divisible by is greater than 50. Hence the smallest prime it could be divisible by must also be greater than 50.
We’re only left with choice E.
For every positive even integer n, the function h(n) is defined to be the product of all the even integers from 2 to n, inclusive. If p is the smallest prime factor of h(100) +1, then p is? Alternate Solution.
There’s another way to tackle to this one.
You can start from the answers focusing on prime numbers. You’ll notice that there aren’t many options for primes given the constraints in the answer choices (only 12 primes). Also, these primes up to 37 should be familiar ones.
Confused about what a prime is? Having trouble recalling the primes up to 37? Dig in and get this basic quant content sorted!
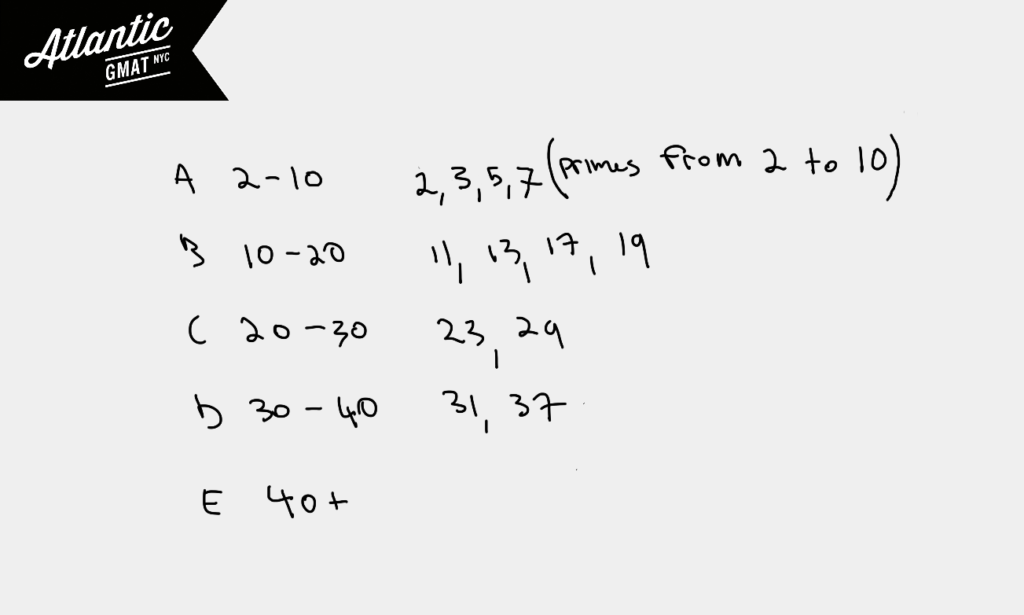
Now let’s go back to our 100! and our divisibility rule and consider if any of these primes are factors. Let’s remember that our 100! only contains the evens so it’s composed of 2 x 4 x 6 x 8 x 10 x 12 x 14 x 16 x18 x 20 x 22 x 24 x 26 x 28…90 x 92 x 94 x 96 x 98 x 100.
Is 100! (only the even numbers) divisibly by 2? Yes. Is 1 divisible by 2? No. Then is 100! + 1 divisible by 2? No!
Is 100! (only the even numbers) divisible by 3? Yes. Is 1 divisible by 3? No. Then is 100! + 1 divisible by 3? No!
Is 100! (only the even numbers) divisible by 5? Yes. Is 1 divisible by 5? No. Then is 100! + 1 divisible by 5? No!
That eliminates A. You can also see that our list of products contains 11, (11 x 2 = 22), 13 (13 x 2 = 26), 15 (15 x 2 = 30) and so on.
Video Solution: For every positive even integer n, the function h(n) is defined to be the product of all the even integers from 2 to n, inclusive. If p is the smallest prime factor of h(100) +1, then p is?
You don’t need to get this correct (or any other super tough question) but you do need to understand the steps
Easy! Not quite.
This is a very puzzle-y GMAT question and one of the toughest of the tough. I would expect very few people to get this one right first time around. I certainly did not and I almost always score a 49 on the quant.
Still, it doesn’t require any complicated formulas or crazy math knowledge. It’s also lightweight in terms of calculations.
Do you need to solve this in order to get a 700+ GMAT score?
No. But, the lessons contained in the solution of this question are important.
So even though there’s no need to stress about solving something like this on your exam I would spend some time thinking about this solution making sure that every step feels logical.
This is the same type of reasoning that you’ll be using everywhere on the GMAT.
More GMAT Function Example Questions
Here are two more GMAT function questions that are still challenging but now quite as tough as this one. They are very formulaic so make sure you’ve got them 100% as they do come up almost exactly in this form:
For which of the following functions is f(a+b) = f(b) + f(a) for all positive numbers a and b?
For which of the following functions f(x)=f(1-x)
Happy studies!