A certain office supply store stocks 2 sizes of self-stick notepads, each in 4 colors: Blue, Green, Yellow or Pink. The store packs the notepads in packages that contain either 3 notepads of the same size and the same color or 3 notepads of the same size and of 3 different colors. If the order in which the colors are packed is not considered, how many different packages of the types described above are possible?
(A) 6
(B) 8
(C) 16
(D) 24
(E) 32
Here’s a challenging combinatorics question from the GMAT Prep Tests. We almost always see the self-stick notepad question come up in the lifecycle of a GMAT prep here at Atlantic. There’s not much work to do as the office supply store only stocks two sizes and four colors (limited options should signal the possibility of just writing out the scenarios). Keep in mind that most of this question (and many GMAT questions) relies on simply understanding the text and then getting the information organized.
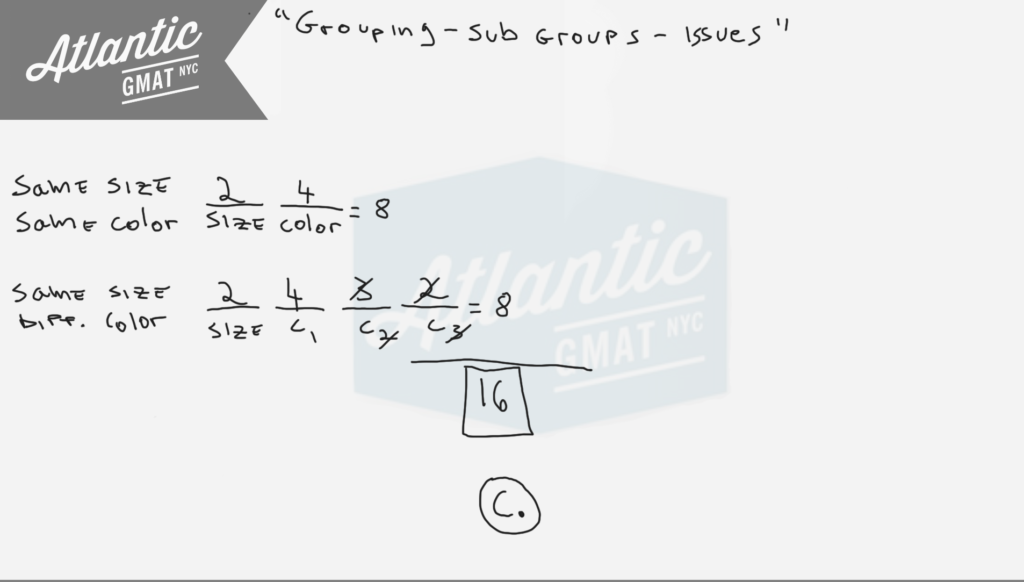
Yes, it is helpful to have some basic combinatorics tools. But that aspect of this question is really lightweight as you can see in the diagram below.
Office Supply Store Self-Stick Notepads Solution!
Table of Contents
The first step is to figure out the number of self-stick notepads that have the same size and same color. Set up one slot for size and the other for color. Then do the same things for same size but different color. This part is a little tricker as you need to consider the color aspect more specifically.
For the first pad you can choose all 4 colors. But for the second, because you can’t use the same color that you chose for the first notepad, you can only choose 3 colors. For the third pad you can choose 2 colors. You need a denominator for the colors because you are making a group (order doesn’t matter). So you need to divide out the duplicates (green, blue, yellow is the same as blue, green, yellow so you shouldn’t count both of those).
Because you don’t have that many options this could be a question on which you might avoid formulas altogether and just write out the scenarios or do some combination of practical and formula.
Here is the solution with the slot method described above:
Here’s a practical approach to counting these self-stick notepads
Different Size – Same Color
Size 1 notepads in 4 colors (all blue, all green, all yellow, or all pink) = 4 options
Size 2 notepads in 4 colors = same as size 1 = 4 options
Total = 8
Different Size – Different Color
Size 1 ABC, ABD, ACD, CBD
Size 2 SAME COLOR POSSIBILITIES AS SIZE 1
Total = 8
8 + 8 = 16.
Here’s another multi-step challenging GMAT Combinatorics question with an in depth explanation:
Tanya prepared 4 different letters to be sent to 4 different addresses.