A set of 15 different integers has median of 25 and a range of 25. What is greatest possible integer that could be in this set?

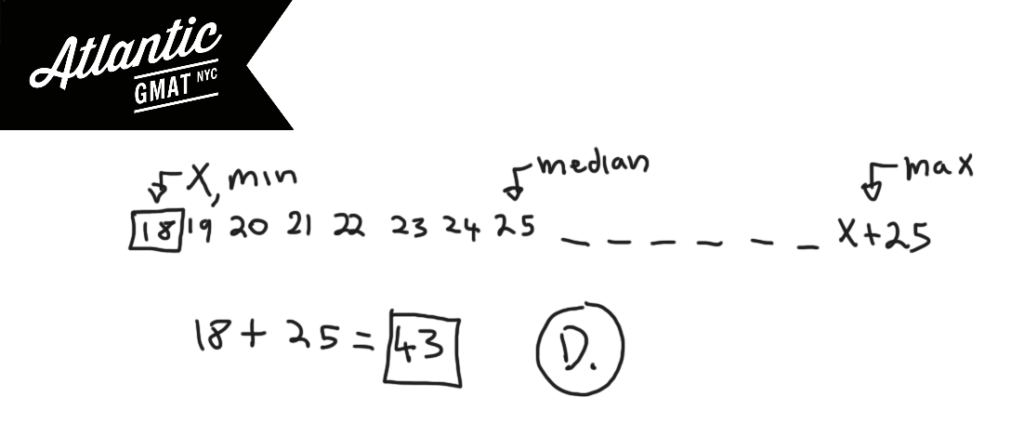
(A) 32
(B) 37
(C) 40
(D) 43
(E) 50

Ready of a GMAT statistics puzzle? Foggy on median and range? Go back to the GMAT basics! Get this fundamental GMAT content down backwards and forwards so that you can focus on the critical thinking portion of the exam.

What is Median?

Median is the middle number of an odd set or the average of the two middle numbers of an even set.

What is Range?

Range is the biggest number minus the smallest number (Range = max – min).

Let’s get organized!

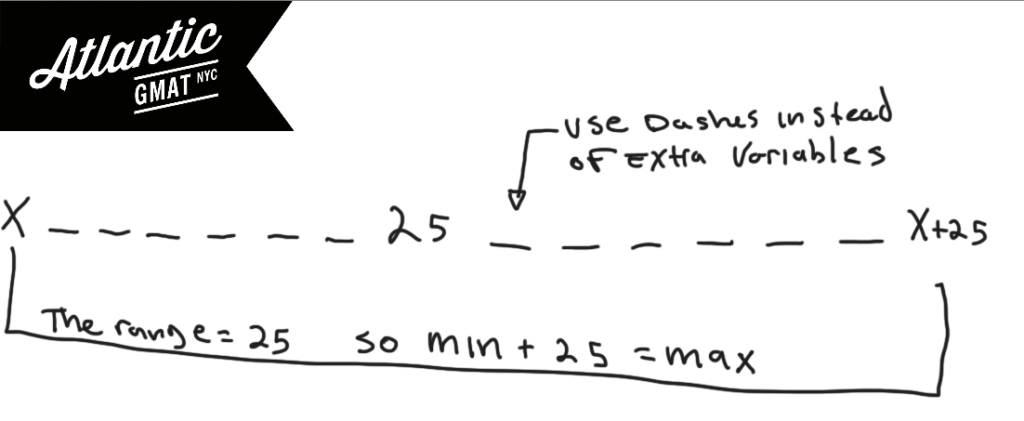
Let’s start by plotting out what we know. Median is spatial so demands a diagram. In a set of 15 numbers the median is the 8th number (7 above it, 7 below it). Especially for statistics set questions avoid creating a million variables for numbers you’re not solving for. Let’s represent those numbers with dashes and create a variable for the min. Then you can add 25 to that for the max. Keep in mind what we’re solving for: the greatest possible integer that could be in this set.

We know the range is 25 and that we want to make the max as big as possible. So what should we do with the min? We want to make the min as big as possible so that min + 25 (the max) is as big as possible. You think: let’s make the min = median. Good thinking!

That would be perfect. But that’s not possible as it is a set of 15 different integers. Still, we’re on the right track. Let’s just go down as little as possible from the median. 24.9999999999. Good thinking again! But, we have to stick with integers. So then you’ve got 24, 23, 22, 21, 20, 19, 18. Add 25 to 18 and that’s the greatest possible integer in the set.

Additional GMAT Statistics Example Questions!

Here’s a mini-statistics puzzle from the GMAT Official Guide. It has a very simple solution. Still, it’s surprising how often it comes up in tutoring sessions.

If Q is an odd number and the median of Q consecutive integers is 120, what is the largest of these integers?

Here’s a challenging statistics, max/min question which we review in just about every GMAT preparation. it’s a great one to master not only to understand how to organize a whole bunch of potential variables but to understand how to put context on a max/min scenario.

Seven pieces of rope have an average (arithmetic mean) length of 68 centimeters and a median length of 84 centimeters. If the length of the longest piece of rope is 14 centimeters more than 4 times the length of the shortest piece of rope, what is the maximum possible length, in centimeters, of the longest piece of rope?

Kind of a basic GMAT statistics question. Not the most challenging but it is still very important to be ready to interpret a chart/graph. What isn’t challenging in practice can quickly become a mess on test day.

The table above shows the distribution of test scores for a group of management trainees. Which score interval contains the median of the 73 scores?

Great one to wrap your head around statistics concepts and how they can be tested on the GMAT. It’s a problem solving question but having this square will also help you on DS statistics questions.

Last month 15 homes were sold in Town X. The average (arithmetic mean) sale price of the homes was $150,000 and the median sale price was $130,000. Which of the following statements must be true?

Middle difficulty DS statistics range question from GMAT question of the day

And here’s a very challenging GMAT statistics range question from GMAT question of the day that also incorporates a bunch of algebra and number properties. Stay organized!

Good luck and happy studies!