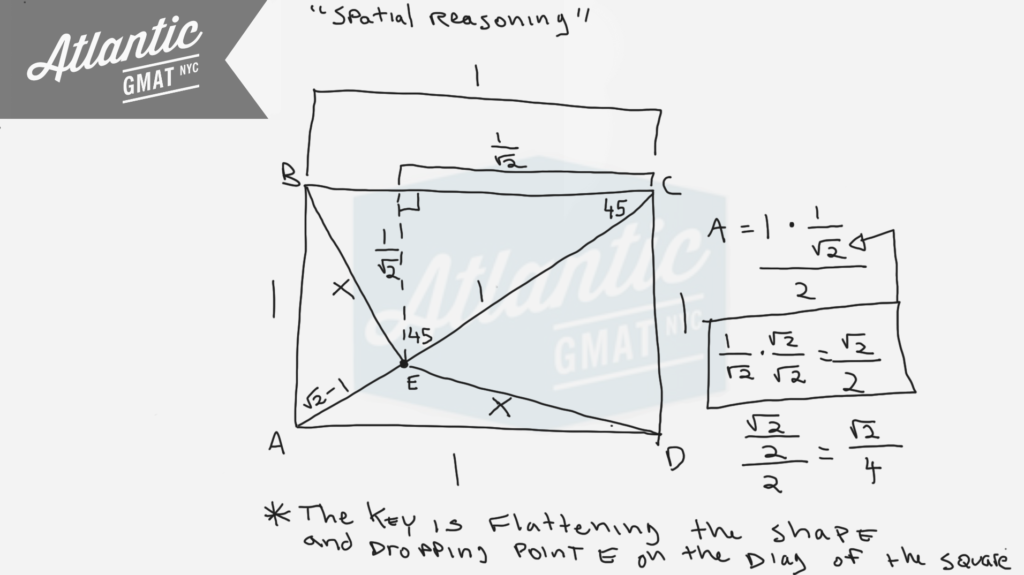
In the figure above, each side of square ABCD has length 1, the length of line segment CE is 1, and the length of line segment BE is equal to the length of line segment DE. What is the area of the triangular region BCE?
(A) 1/3
(B) √2/4
(C) 1/2
(D) √2/2
(E) 3/4
This is a tough geometry question from the GMAT prep tests (I think it’s from exam pack 1, tests 3/4). The first time I saw this one I made the mistake of assuming a 3 dimensional figure. The question is much easier once you put the shape in 2 dimensions dropping point E onto the diagonal of square ABCD. At that point it becomes a set of somewhat straightforward inferences. Again, this is a very difficult question and a great majority of people won’t get it correct. So don’t worry if you get a little lost. What’s key is seeing that the solution is basic. There’s isn’t any difficult math involved. The tough part is figuring out what the question is telling you.
What is the area of the triangular region BCE? Let’s figure it out!
There are two important inferences to make:
- For a square always define the diagonal. It comes up a ton on GMAT geometry questions.
- If you’re looking for the area of a triangle you’ll need a height. If not dealing with a right triangle go ahead and always draw an altitude/height.
Once you’ve done those two things finding the area of the triangular region BCE is a piece of cake.
More challenging GMAT geometry questions with right isosceles triangles
Here is another challenging geometry question with 45-45-90 triangles: The perimeter of a certain isosceles right triangle is 16 + 16√2. What is the length of the hypotenuse of the triangle?
And another: In the figure above, is the area of triangular region ABC equal to the area of triangular region DBA?
And finally a right isosceles triangle example from GMAT question of the day.