Quick Sell Outlet sold a total of 40 televisions, each of which was either a Model P television or a Model Q television. Each Model P television sold for $p and each Model Q sold for $q. The average (arithmetic mean) selling price of the 40 televisions was $141. How many of the 40 televisions were Model P televisions? GMAT Explanation + Additional Examples!
Quick Sell Outlet sold a total of 40 televisions, each of which was either a Model P television or a Model Q television. Each Model P television sold for $p and each Model Q sold for $q. The average (arithmetic mean) selling price of the 40 televisions was $141. How many of the 40 televisions were Model P televisions?
(1) The Model P televisions sold for $30 less than the Model Q televisions
(2) Either p = 120 or q = 120
Define the question! How many of the 40 televisions were Model P televisions?
Table of Contents
As usual, we start from the end to define what the question asks for. This time, it’s pretty straightforward – how many Model P televisions are there?
Organize the information: Put together some equations
This question gives a lot of information right off the bat, so let’s break down what quantities we are dealing with here. Let’s start with what we know:
First, we have a total of 40 televisions, with some being Model P and the rest being Model Q. Let’s call the number of Model P televisions ‘x’ and the number of Model Q televisions ‘y’. So:
We also know that the average selling price of the TVs is $141. Let’s define that with an equation using the average formula:
We can be more explicit with the total money made by thinking in terms of each model separately.
We have the price for each model of TV: Model P is p dollars and Model Q is q dollars.
So the full equation looks like this:
Or by multiplying by 40 on both sides, it looks like this:
In total, we have two equations here with 4 unknown variables.
Unless there’s something special going on we are going to need at least two more equations to solve for the number of Model P televisions.
Let’s take a look at statement 1.
(1) The Model P televisions sold for $30 less than the Model Q televisions.
We can write this as:
Since this only gives us one additional equation, we won’t be able to solve for X with this statement alone.
Insufficient.
Let’s look at statement 2.
(2) Either p = 120 or q = 120.
While this appears to give us two additional equations, the “Either…or” means only one of these is actually true. We don’t know which.
So it’s only one additional equation but even then not helpful unless we can determine which scenario applies.
Insufficient.
Let’s look at both statements.
Taken together, we have:
Either or
Even though it looks like we have a sufficient number of equations, we might not be in the clear. Why?
As mentioned, the “Either…or” statement suggests that either could be true, meaning there might be two different solutions for X.
This requires an additional step to see if we can rule out one of the equations in statement 2. If we can we’ll be sufficient. If not we’re insufficient
Let’s look at the two equations that share variables in such a way that we can solve.
or
.
Therefore, we have one of:
and
OR
and
.
What else do we know?
Let’s think back to the original question: the average selling price is $141.
The average selling price has to be somewhere between the two prices — it’s an average!
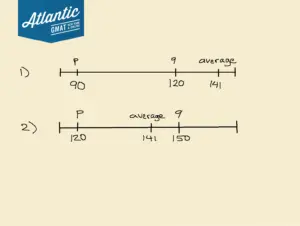
That rules out p = 90/ q = 120 because 141 is out of that range.
Let’s see this in a diagram:
In option 2, the average is clearly between the two prices, whereas in option 1, the average is out of range. So now we know for sure that p = 120 and q = 150.
Now we actually have four equations and four variables. This can definitely be solved!
Here’s a simplified version with p and q substituted in. You can see that by substitution or adding/subtracting equations you’ll be able to solve for one variable.
So both statements together are sufficient.
Answer: C