On the number line, the distance between x and y is greater than the

On the number line, the distance between x and y is greater than the distance between x and z. Does z lie between x and y on the number line? GMAT Explanation + Additional Practice!

On the number line, the distance between x and y is greater than the distance between x and z. Does z lie between x and y on the number line?

(1) xyz < 0

(2) xy < 0

 

Define the question: Does z lie between x and y on the number line?

Not too much else to note here.

 

Organize the information with some number lines:

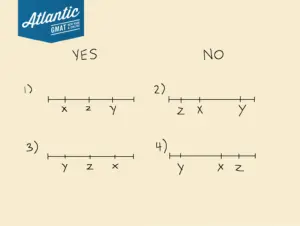
We know that y is farther from x on the number line than z is. Let’s draw out some diagrams to visualize all the possible configurations of x, y, and z on the number line. 

Here are all four possibilities:

on the number line, the distance between x and y is greater than the distance between x and z

Here, we have two number lines where z is between x and y (those in the YES column) 

AND

two number lines where z is not between x and y (those in the NO column). 

I’ve labeled each one with a number 1 – 4 for easy reference. 

If one of the statements narrows things down to one column (either yes or no) then it’s sufficient. If it’s possible to have scenarios in either column then the statement is insufficient.

 

Let’s put together a strategy to determine whether we have sufficient data. 

  • If we can find a “YES” number line that works with the additional statements and not a “NO” number line, we know the answer is yes — the data is sufficient.
  • If we can find a “NO” number line that works and not a “YES” number line, we know the answer is no, so we have sufficient data. 
  • If neither or both “YES” and “NO” number lines work with the additional statements, we have insufficient data.

 

Let’s take a look at statement 1

 

(1) xyz < 0

What does that tell us about these numbers? 

You’ll need to lean a bit on your number properties rules related to polarity (positive/negative).

How is the product of three numbers negative? 

– * – * – = –

– * + * + = –

 

So either one or all three numbers are negative.

Let’s try to place 0 somewhere on the number line to satisfy this condition on both a “YES” and “NO” number line.

on the number line, the distance between x and y is greater than the distance between x and z - statement 1

 

By just placing a 0 to the right of all three numbers, we can satisfy this condition with both “YES” and “NO” number lines. Therefore, statement 1 is insufficient.

Let’s try statement 2.

 

(2) xy < 0

This statement tells us the product of x and y is negative. In other words, either x is negative or y is negative. Again, let’s try to place 0 somewhere that satisfies this statement on both a “YES” and “NO” number line:

on the number line, the distance between x and y is greater than the distance between x and z - statement 2

 

Here, we can just place a 0 anywhere between the x and the y on any number line to satisfy this statement. So, statement 2 is insufficient.

 

Let’s try both statements together:

Here’s where things get interesting. Statement 1 says either 1 or 3 numbers have to be negative, but statement 2 says only one of x and y can be negative. 

Since the other one or x or y needs to be positive, we can’t have 3 negative numbers. We can only have 1 negative number, and this needs to be either x or y from statement 2.

Let’s go back to our number lines and try to place 0.

on the number line, the distance between x and y is greater than the distance between x and z - both

 

Again, we can find both at least one “YES” and “NO” number line that satisfy both statements 1 and 2.

Even considering both statements together, we have found number lines where z does lie between x and y and number lines where z does not lie between x and y. So, both statements together are insufficient.

Answer: E