In the sequence shown, a_n = a_(n−1) + k, where 2 ≤ n ≤ 15 and k is a nonzero constant

In the sequence shown, $a_n = a_{n-1} + k$ , where $2 \le n \le15$ and k is a nonzero constant. How many of the terms in the sequence are greater than 10? GMAT Explanation

Given a sequence: $a_1, a_2, a_3, ... a_{14}, a_{15}$

In the sequence shown, $a_n=a_{n-1} + k$ , where $2 \le n \le 15$ and k is a nonzero constant. How many of the terms in the sequence are greater than 10?

(1) $a_1 = 24$
(2) $a_8 = 10$

GMAT Sequences

Table of Contents

Let’s start off with a quick overview of sequences to break down this question a little a bit.

First things first, what are sequences? All they are is a list of numbers that follow some pattern.

Let’s look at the sequence from the question: $a_1, a_2, a_3, ... a_{14}, a_{15}$ . Here, $a_1, a_2, a_3,$ etc. are the numbers in the sequence, and their subscript (the 1 in $a_1$ , for example) shows their placement within the sequence. $a_1$ comes first, $a_2$ comes second, and so on.

We also have a pattern defining the sequence: $a_n$ = $a_{n-1} + k$ . What is $a_n$ ?

Well, $a_n$ simply means the “nth” spot in the sequence. If n is 3 for example, then it’s $a_3$ , or the third number in the sequence. And in this question, we have 2 ≤ n ≤ 15, so $a_n$ can be anything from $a_2$ to $a_{15}$ .

That covers $a_n$ , but what about $a_{n-1}$ ?

$a_{n-1}$ just means the number before the “nth” spot. So if n is 3, $a_{n-1}$ is $a_2$ , or the second number in the sequence. And again, we have 2 ≤ n ≤ 15, so $a_{n-1}$ can be anything from $a_1$ to $a_{14}$ .

Here’s a good graphic from Wikipedia’s page on sequences to sum this all up.

sequence explanation — Sequence Explanation from Wikipedia

Define the question: How many of the terms in the sequence are greater than 10?

Sounds pretty straightforward. We just need to find how many numbers in our sequence $a_1, a_2, ... a_15$ are greater than 10.

Organize the information: What does our pattern tell us?

Most of the information we’re going to get here comes from the pattern: $a_n = a_{n-1} + k$ . First, let’s talk about n and k.

Let’s start with n. We know that 2 ≤ n ≤ 15. So we also know that 2 – 1 ≤ n – 1 ≤ 15 – 1, which is the same as 1 ≤ (n – 1) ≤ 14.

What does our pattern looks like plugging in difference values of n? We’ll start with n = 2, 3, and 4

n=2: $a_2 = a_1 + k$

n=3: $a_3 = a_2 + k$

n=4: $a_4 = a_3 + k$

After plugging in a few examples, let’s see if the pattern here makes a bit more sense. We have $a_1$ plus some number k gives $a_2$ . $a_2$ plus the same number k gives $a_3$ . And again, $a_3$ plus some number k gives us $a_4$ . In other words, to get from one number in the sequence to the next, we just add k!

Well what do we know about k?

The question says k is a nonzero constant. Let’s start with the “nonzero” here. All this means is k can be any number other than 0. k could be any positive or negative number, anything except 0.

We also know k is constant. That’s exactly what it sounds like — k doesn’t change. In our pattern, $a_n = a_{n-1} + k$ , k will be the same regardless of n. We are always adding the same k to get to the next number of the sequence.

With all this in mind, let’s check out the statements.

(1) $a_1 = 24$

Statement 1 gives us that the first number in the sequence, $a_1$ , is 24. Can we use this to figure out how many numbers in the sequence are greater than 10?

Well, that depends on what k is. Since this statement doesn’t tell us anything about k, let’s pick different values for k and see how that affects how many numbers are greater than 10.

For example, let’s pick k = 1. Since $a_1 = 24$ , $a_2 = a_1 + 1 = 25$ . $a_3 = a_2 + 1 = 26$ . And so on.

With k = 1, the numbers in the sequence are going to keep getting larger, so every term in the sequence will be greater than 10. So we would have 15 terms of the sequence are greater than 10.

Now, let’s pick a different value for k. Let’s say k = -24. Then, we’d have $a_2 = a_1 - 24 = 0$ and $a_3 = a_2 - 24 = -24$ . And so on.

With k = -24, we have that the second term is 0 and every term after that will become more and more negative. So we have only one term, $a_1$ that is greater than 10, rather than 15 as with k = 1.

Since different choices of k give different answers to our question, we do not have enough information with statement 1 alone.

Insufficient.

(2) $a_8 = 10$

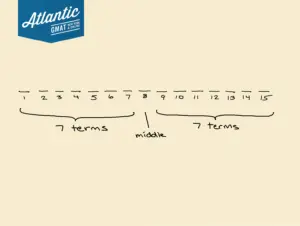
Statement 2 gives us information about the 8th term of the sequence. This might seem like a random choice, but this actually has some significance.

We know our sequence has 15 terms, which means that the 8th term is right in the middle! Here’s a quick diagram showing why that is:

So why is knowing the middle term helpful? Let’s plug in different values of k again to see why that is.

Let’s say k = 1 again. Going back to the pattern, we have $a_9 = a_8 + 1 = 11$ , $a_{10} = a_9 + 1 = 12$ , etc.

We can also use the pattern to go in the opposite direction. $a_8 = a_7 + 1$ , or $a_7 = a_8 - 1 = 9$ . Similarly, $a_7 = a_6 + 1$ , or $a_6 = a_7 - 1 = 8$ .

Let’s think about the whole sequence now.

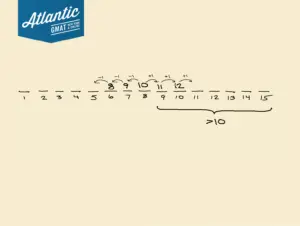
Since we know the middle term $a_8$ is 10 and we have k = 1, we know every term after $a_8$ is going to be positive. Counting the number of terms in the picture above, we have 7 terms greater than 10 here.

This is also true for any positive value of k. Since $a_8$ is 10, any positive value of k will make $a_9$ and the following terms greater than 10 because $a_9$ is 10 plus some positive number. So for any positive value of k, we know 7 terms are greater than 10.

What about negative values of k? Let’s try it out.

Start out with something simple, k = -1. Now, we have $a_9 = a_8 - 1 = 9$ , $a_10 = a_9 - 1 = 8$ , etc.

Going the opposite direction, we have $a_8 = a_7 - 1$ or $a_7 = a_8 + 1 = 11$ . And again, $a_7 = a_6 - 1$ or $a_6 = a_7 + 1 = 12$ . And so on.

Let’s look at this as a diagram again.

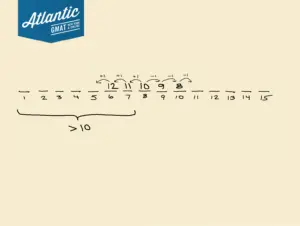
In this case, now we have every term before $a_8$ is greater than 10. Counting the number of terms here, again we get 7 terms greater than 10! And like before, this is true for every negative value of k. Why? Let’s think in terms of the pattern.

If we have $a_8 = a_7 + k$ , we can subtract k from both sides to get $a_7 = a_8 - k$ . With $a_8 = 10$ and k being some negative number, we have $a_7 = 10 - \text{ some negative number}$ , or $a_7 = 10 + \text{some positive number}$ . So, $a_7$ will be greater than $a_8$ , $a_6$ will be greater than $a_7$ , and so on. For any negative k, all 7 terms before $a_8$ will be greater than 10.

We’ve shown that for both positive and negative values of k, we have 7 terms of the sequence greater than 10. And since k is nonzero, we’ve covered all our bases! So statement 2 alone was sufficient.

Correct Answer: B