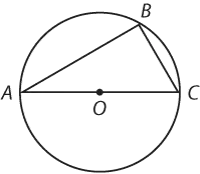
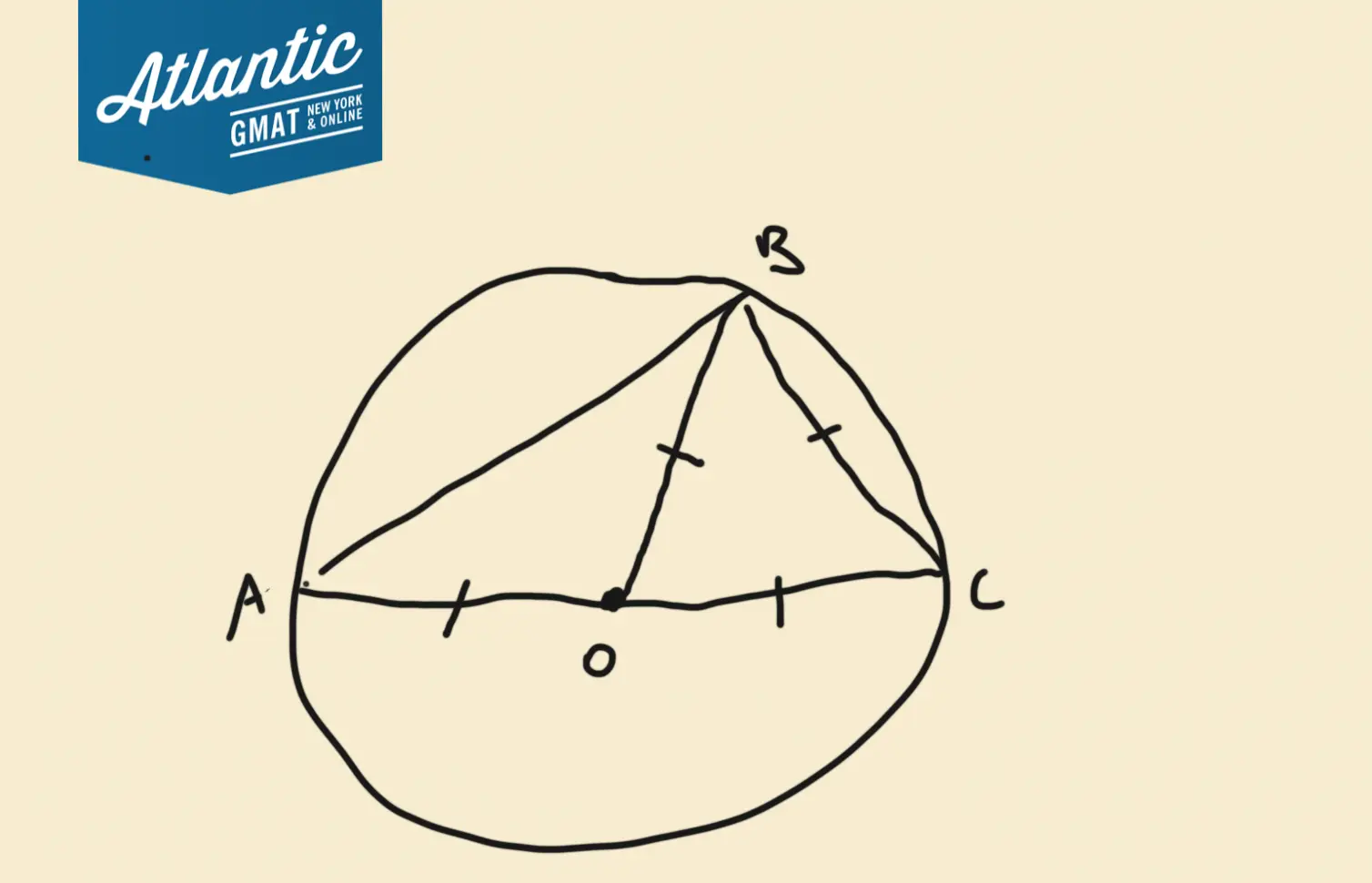
In the figure above, the radius of the circle with center O is 1 and BC = 1. What is the area of triangular region ABC? GMAT Explanation + Additional Examples!
In the figure above, the radius of the circle with center O is 1 and BC = 1. What is the area of triangular region ABC?
(A) √2/2
(B) √3/2
(C) 1
(D) √2
(E) √3
Define the question: What is the area of triangular region ABC?
Table of Contents
Not much to define but I would recommend jotting down the formula for the area of a triangle.
Yes, it’s not complicated and I know that you know it. Still, it’s good to have it in front of you.
That goes for all formulas on the GMAT (except standard deviation!). As they come up in a question: write them out.
Here we go:
Area of a triangle = (Base*Height)/2
Remember: GMAT geometry questions (and most other GMAT questions) follow basic rules, so let’s keep it simple!
An important GMAT Geometry Rule you need to know
Here’s an inscribed triangle/circle rule I’d memorize:
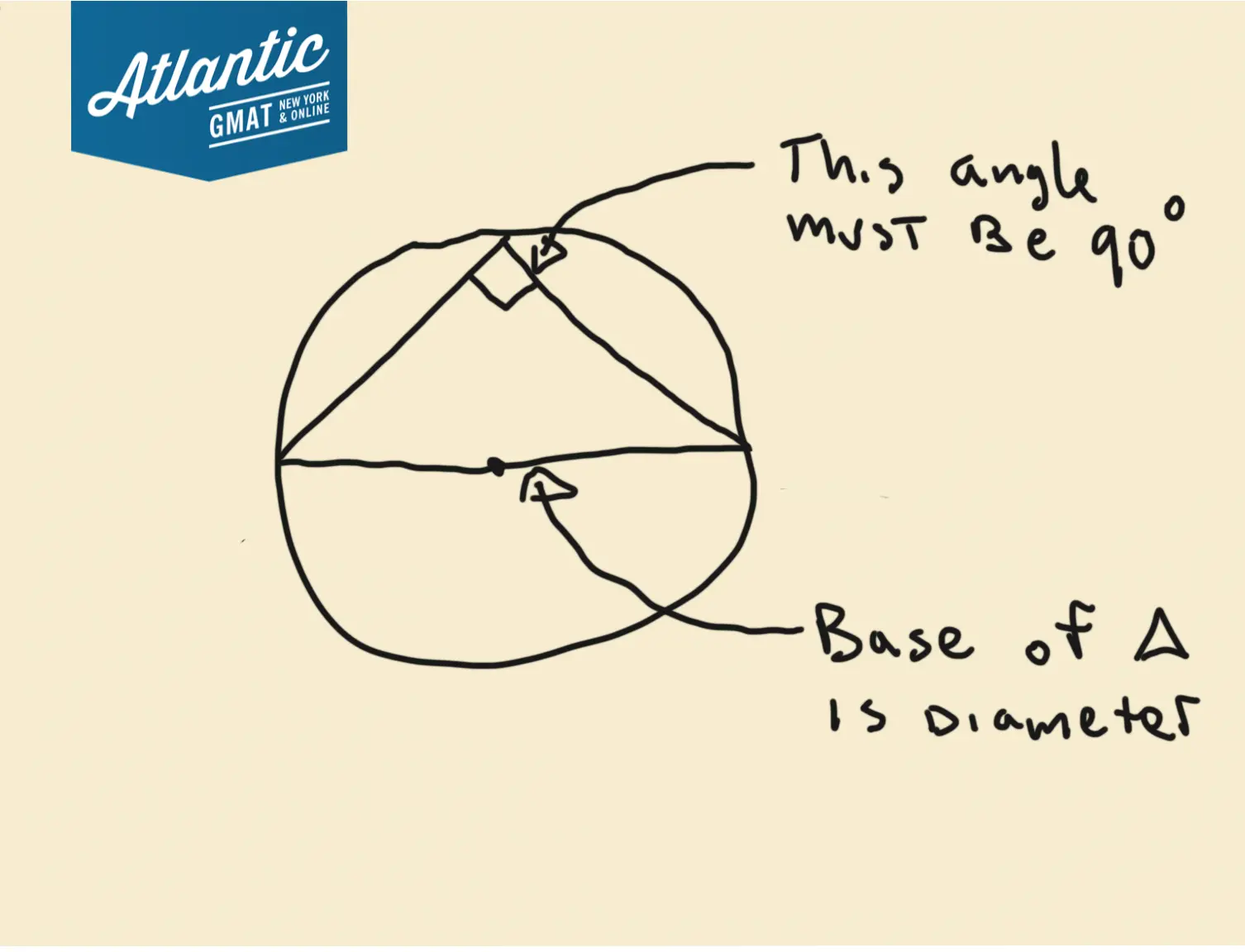
If a side of an inscribed triangle is also the diameter of a circle, the angle opposite the diameter is a right angle.
Let’s apply the inscribed triangle rule to triangle ABC
Are any sides in the diagram a diameter of circle O?
That’s right, Side AB.
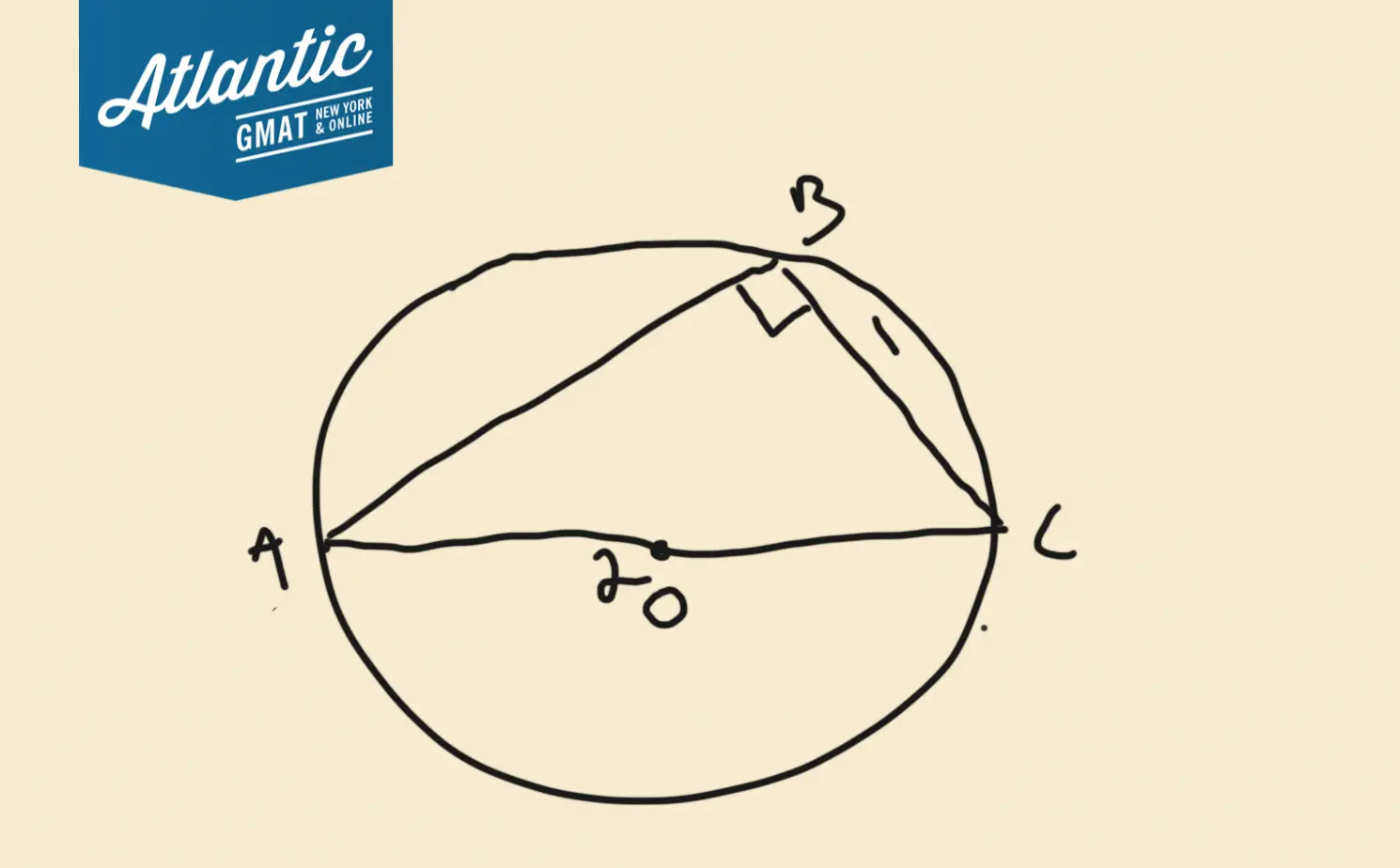
We have a right triangle and the measure of two sides so: pythagorean theorem.
Here’s a diagram of what we know so far:
Time for Pythagorean Theorem
Just to refresh, here’s the Pythagorean Theorem:
a^2 + b^2 = c^2
The “c” is always the largest side which is opposite the 90 degree angle (in this case, AB).
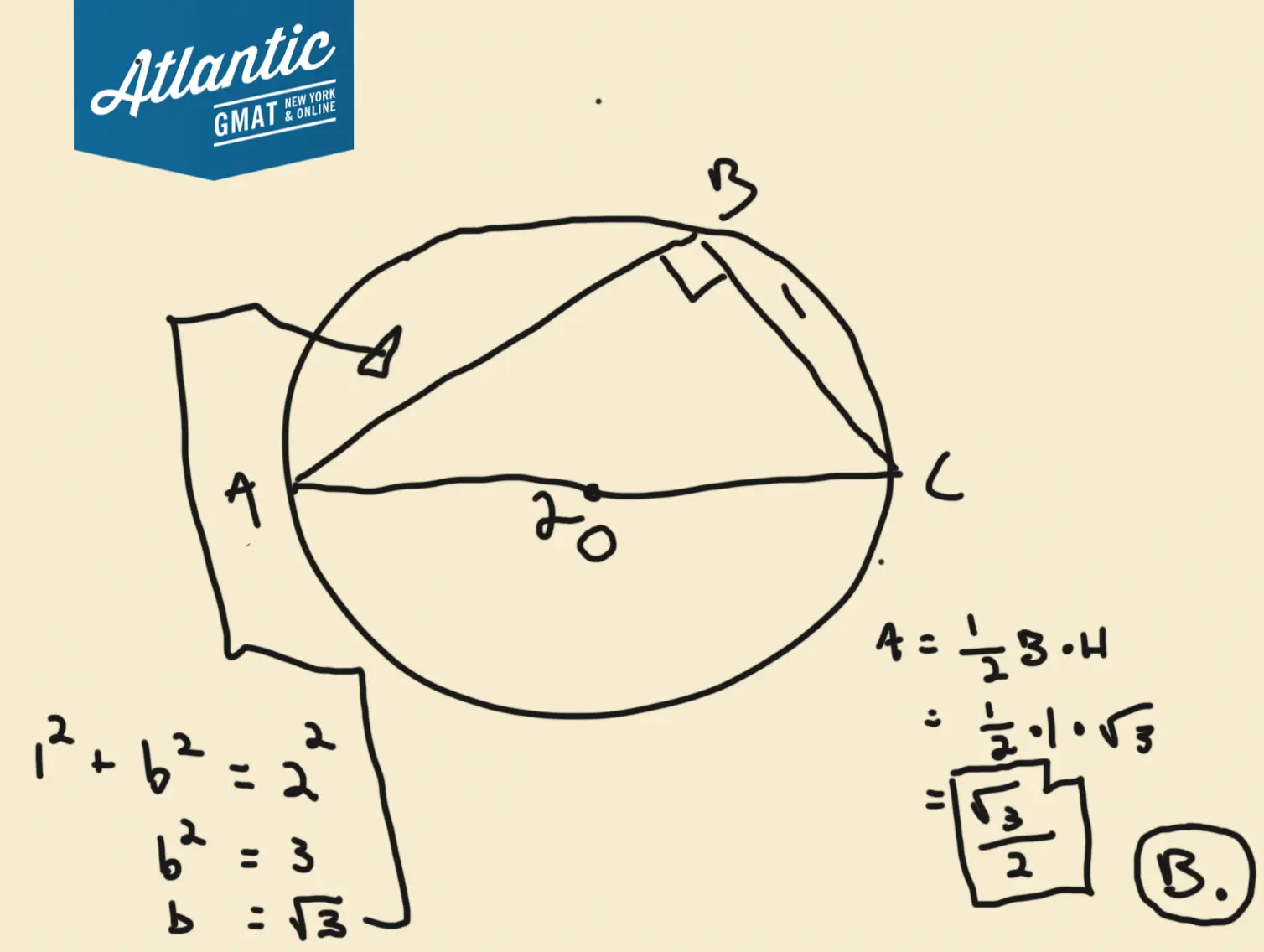
Crunch the numbers:
1^2 + b^2 = 2^2
1 + b^2 = 4
b^2 = 3
b = √3
Side AB = √3
Let’s get back to the question: the area of ABC
Area = ½ * base * height
Area = ½ * 1 * rad 3
Area = √3/2
And done! √3/2 is the area of triangular region ABC.
Here’s a diagram of the complete solution
Alternative Explanation
When trying to make inferences on geometry questions, consider how to break up the shape.
Remember, a circle has infinite radii. Just because they’re not drawn doesn’t mean they won’t be helpful.
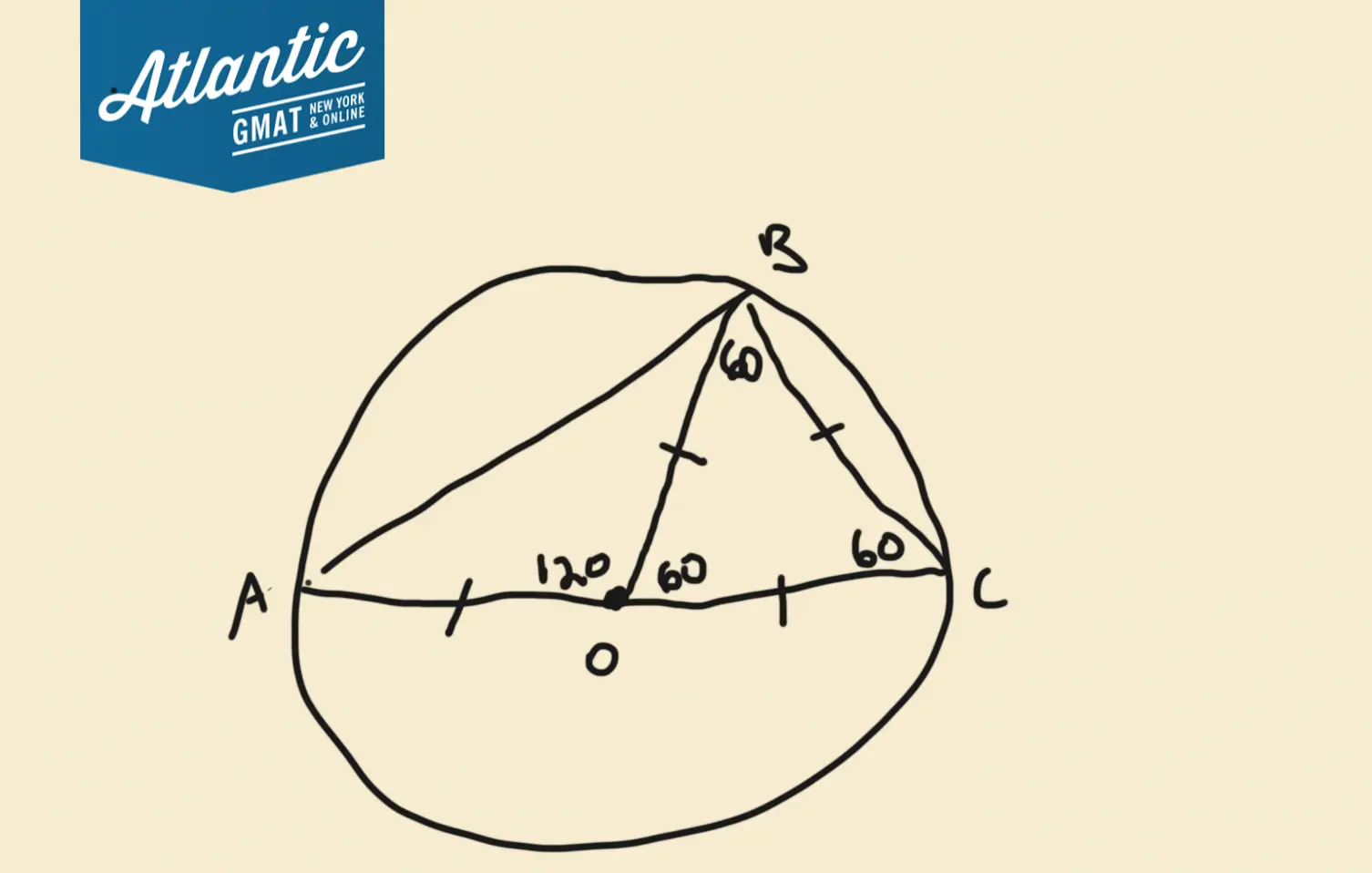
In this case, I’d draw a radii from O to B to create a new triangle.
It’s a helpful triangle, because we know the measurements of all three sides are equal to 1.
What does that tell you about the angles of triangle OBC?
If all sides of a triangle are equal, then all angles are equal to 60
Can we infer the measure of any other angles?
If Angle BOC is 60 degrees,
What’s angle BOA?
180 – 60 = 120
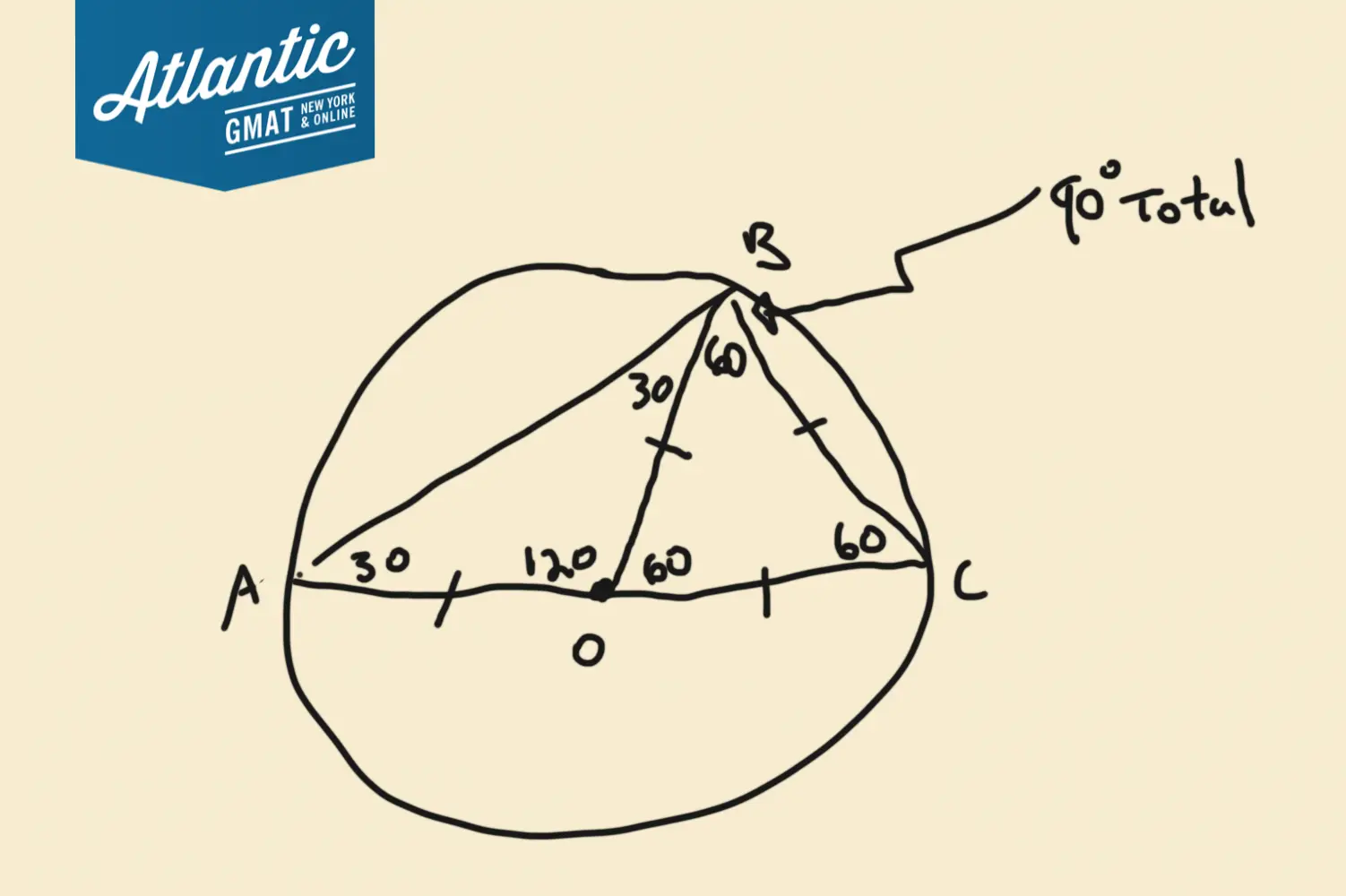
The lengths of side AO and side OB are both 1
So
The angles opposite side AO and OB must be equal (in a triangle same side measure means same angle measure).
180 – 2x = 120
2x = 60
x = 30
Angle BAO and angle ABO are each 30 degrees.
Pythagorean Once Again
Now we have a right triangle and we know 2 sides so can do Pythagorean the same as we did above.
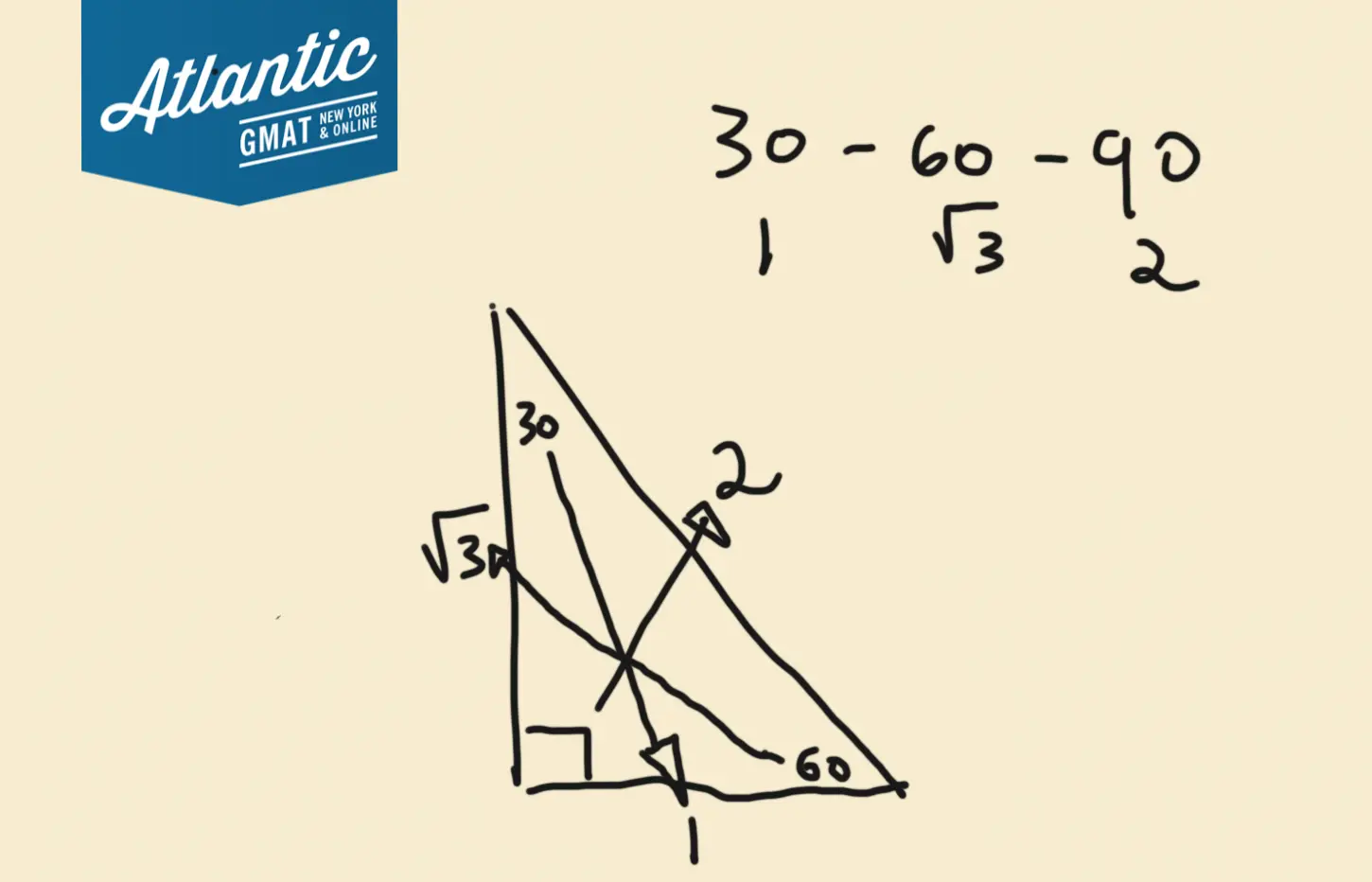
Spotting Special Triangles
The other way to work it is with special triangles. Do any of the angle measurements in triangle ABC look particularly familiar?
Right! Triangle ABC is a 30-60-90 triangle. All 30-60-90 triangles have sides in a ratio of: 1:√3:2
Since AC = 2
And BC = 1
Then side AB must be √3
Back to the question: What is the area of the triangular region ABC?
Area = ½ * b * h
Base = BC = 1
Height = AB = √3
½ * 1 * √3 = √3/2
Correct Answer: B