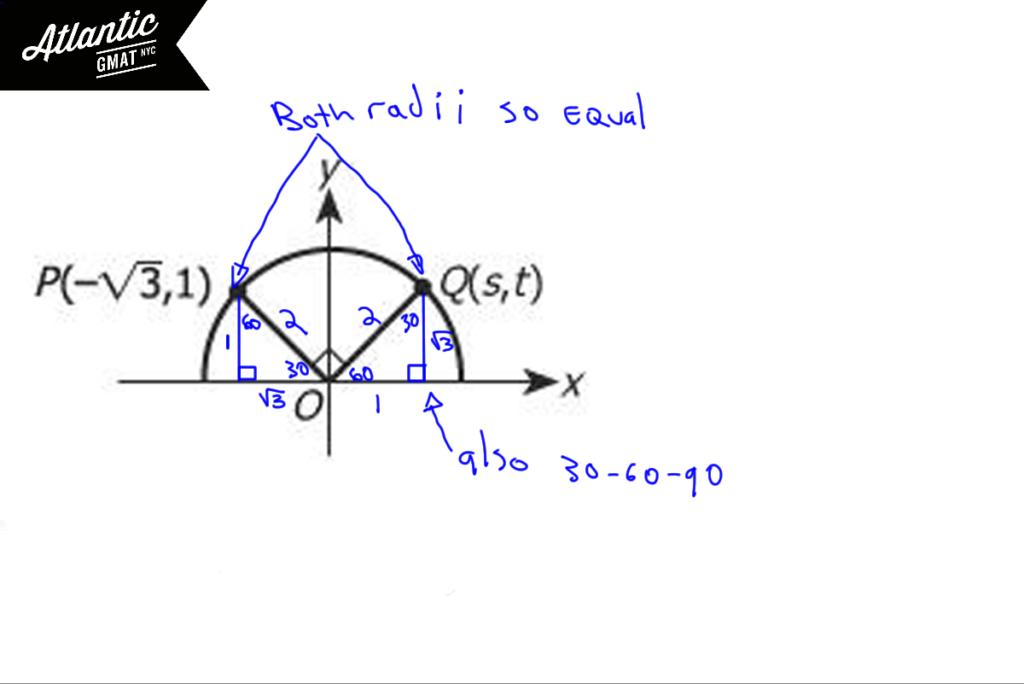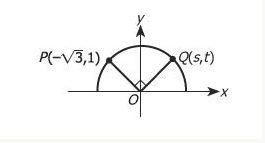
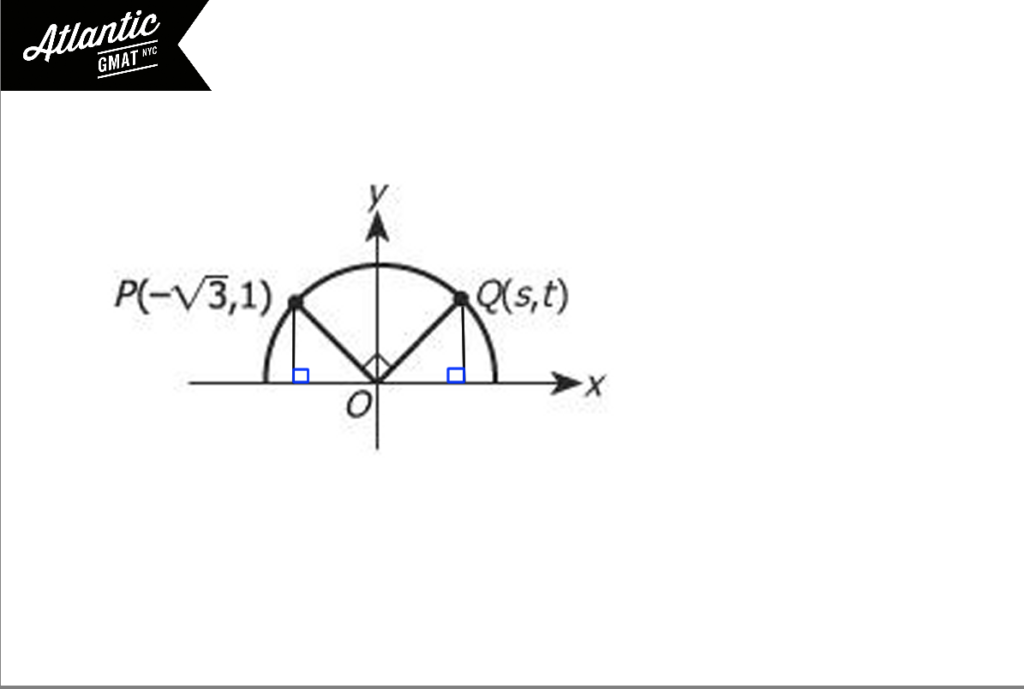
In the figure above, points P and Q lie on the circle with center O. What is the value of s?
A. 1/2
B. 1
C. √2
D. √3
E. √2/2
Statistically this is a challenging GMAT question. A lot of people get it wrong. However, it’s not all that tough. And if you’re gunning for a top shelf GMAT score then better get it right! You need to excel at these statistically tough but actually easy questions. How? Stay organized Don’t make assumptions. With those two things you avoid most GMAT traps. In this circle question most people assume that the figure (the baseball field) is exactly split by the y axis so that the value of s is equal to √3. Is it? Nope. Most GMAT diagrams are drawn to scale but that doesn’t mean that they aren’t misleading. Don’t assume symmetry just because a figure looks symmetrical. It could be .00000001 off. Now, let’s not get paranoid. That doesn’t mean straight looking lines might be curved. Still: avoid making assumptions.
Let’s start organizing this diagram by creating triangles. We can create two tidy right triangles on each side. You can find a video explanation here: In the figure above, points p and q lie on the circle with center O. What is the value of s?
The base on the left must be √3 because of the x coordinate of point P. The height of that triangle must be 1 because of the y coordinate of point P. It’s a right triangle. You have two sides. Can you get the third? Of course! Pythagorean theorem. So that third side is 2. Interesting. If you’ve got your basic GMAT geometry in shape (no pun intended) you should notice that you have 1, √3, 2 and it’s a right triangle. Yep: 30-60-90. Great.
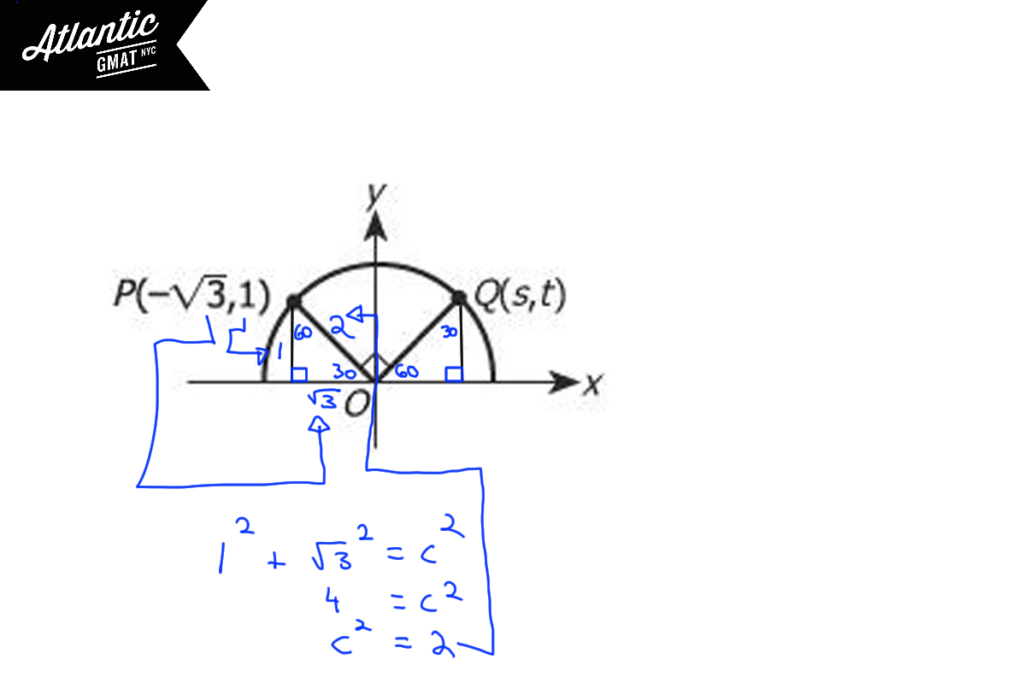
Let’s make more inferences inferences: points P and Q lie on the circle with center O. Always pay attention to radii or draw extra ones as needed. Here, the lines ending in P and Q are equal because both are radii of circle O. So the angle opposite the 1 side must be 30 degrees leaving a balance of 60 degrees for the angle to the right of the 90 degree angle. So angle Q must 30 degrees. Another 30-60-90! So the side opposite the 60 degree angle is √3 and the side opposite the 30 degree angle (what we’re solving for) is 1. Correct answer: B