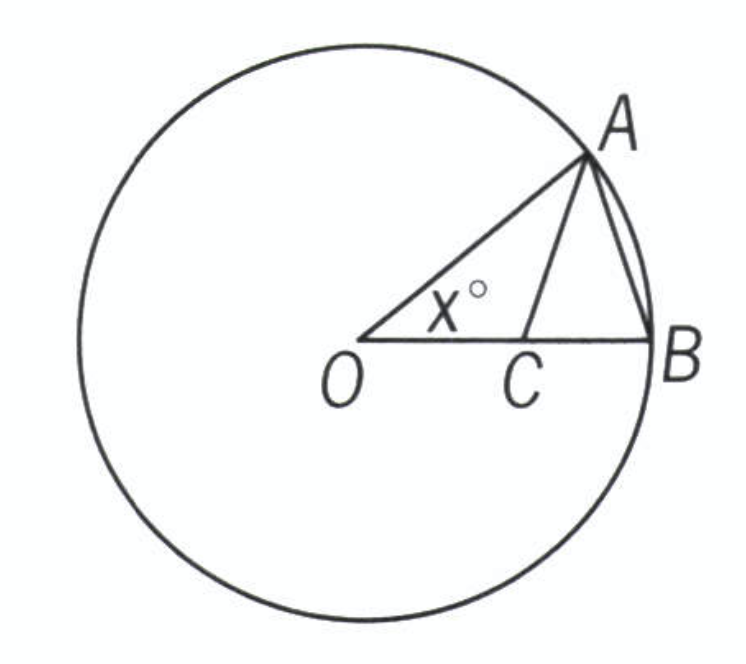
In the figure above, point O is the center of the circle and OC = AC = AB. What is the value of x?
(A) 40
(B) 36
(C) 34
(0) 32
(E) 3
Explanation + a simple rule that will help you on challenging GMAT triangle questions (scroll down for video solution)
This GMAT geometry question from the official guide (quantitative review) hinges on a simple rule that is overrepresented on challenging GMAT geometry questions involving triangles.
What is it?: the exterior angle theorem!
Eh? Sounds complicated but it’s actually pretty basic one you see it in action.
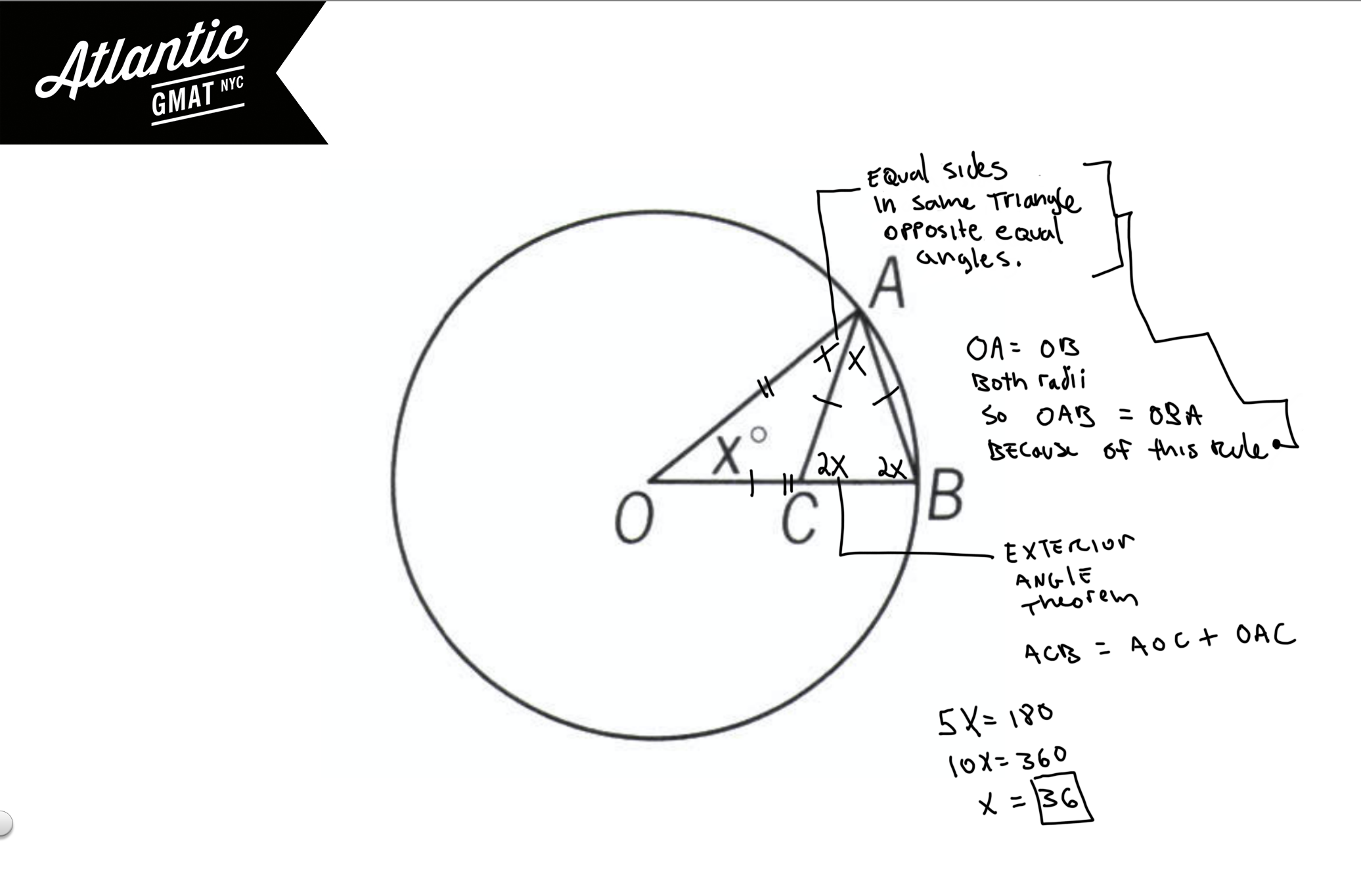
Angle ACB above is an “exterior angle” of triangle AOC. The exterior angle theorem states that the exterior angle ACB equals the sum of the “remote interior angles” OAC and AOC.
Basically, the exterior angle equals the sum of the angles that it’s not connected to, the other two angles of the triangle known as the “remote interior angles”.
If triangles share sides it’s not unlikely that you’ll have an exterior angle and will be able to use (and will probably need to use) the exterior angle theorem. So, keep EAT (exterior angle theorem) in mind.
Here are the steps that I’d follow to solve:
- Draw a diagram and make easy inferences. The first one to label is that OC = AC = AB.
- Once you have those equal sides you can also label angles that are equal as sides that are equal within the same triangle have angles opposite them that are also equal.
- Now you should be thinking, hmmm, triangles sharing sides maybe there’s an exterior angle. Yes, of course there is! Angle ACB. ACB is equal to AOC + OAC.
- Now you should also be wondering why this triangle is in a circle. How can the circle help you make an inference? For GMAT circle questions always think about “helpful radii”. There’s usually a radius whether it’s drawn or you have to draw it that will help. In this case OA and OB are both radii so they are equal boom!
- That’s it. You should have all angles defined by x. Go ahead and sum all of the x’s and set that equal to 180 to solve.