If x, y and z are positive numbers, is z between x and y? GMAT Explanation

If x, y and z are positive numbers, is z between x and y?

(1) x < 2z < y
(2) 2x < z < 2y

 

Define the question: Is z between x and y?

Looking ahead at the statements, we can see this question is dealing with inequalities. Let’s re-express the question in terms of inequalities. We want to know if z is between x and y. Well, this is possible in two different ways:

1. x < z < y
2. y < z < x

As we work through this problem, we need to see if the information we have is enough to prove that either one of these is true.

 

Organize the information:

The only information the question tells us is that x, y, and z are all positive. Let’s move on to looking at the statements with this in mind.

 

(1) x < 2z < y

For a question like this, it’s probably a good idea to see if you can find a counterexample – a choice of values where the statement is true, but z is not between x and y.

Let’s say we have x = 3, 2z = 4, and y = 5.

With these choices, it’s easy to tell that the statement is true: 3 < 4 < 5. But if 2z = 4, then we have z = 2. Since 2 is not between 3 and 5, we found a case where z is not between x and y even though the statement is true.

That means statement 1 is insufficient.

 

(2) 2x < z < 2y

Again, let’s look for a counterexample.

Let’s try 2x = 4, z = 5, and 2y = 6.

Using these values, the statement is true: 4 < 5 < 6. But since 2x = 4 and 2y = 6, we have x = 2 and y = 3. Since 5 is not between 2 and 3, we have a case where z is not between x and y even when the statement is true.

Insufficient

 

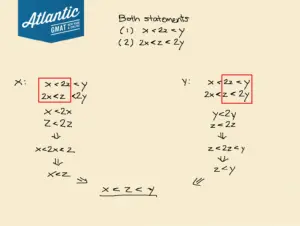
Let’s try both statements together:

At this point, trying to find a counterexample might be difficult since there’s so many values to keep track of and inequalities to satisfy. So let’s try a different approach.

Let’s narrow down the scope of the problem. Do we know anything about the relationship between x and z? Here’s what we know from the statements:

x < 2z

2x < z

 

Since x and z are also both positive, we also know that:

x < 2x

z < 2z

 

Let’s combine this with what we know from the statements. In particular, let’s look at these two:

x < 2x

2x < z

 

Since these inequalities share a 2x, we can combine them to say:

x < 2x < z

 

And by the transitive property of inequality (or simply that x is less than a value that is less than z), we know that x < z.

Let’s see if we can do something similar for y and z? Here’s what we know from the statements

2z < y

z < 2y

 

And again, because y and z are both positive, we know:

y < 2y

z < 2z

 

Let’s take a look at these two inequalities:

z < 2z

2z < y

 

Since these share a 2z, let’s combine them like before:

z < 2z < y

 

Just like before, using the transitive property of inequality, we know z < y.

So now, we have:

x < z

z < y

 

Finally, we can combine these to say:

x < z < y

which shows that z is, in fact, between x and y. Both statements together are sufficient.

Correct Answer: C

 

Here’s that all worked out: