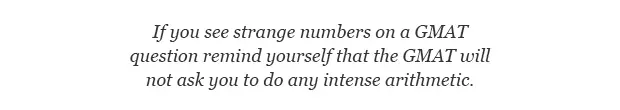Whether you are just starting with your GMAT Prep, deciding whether to take the GMAT, or nearing the test it helps to practice on high quality GMAT sample questions. The best GMAT sample questions are official ones from the creators of the GMAT. Here you can access 90 free GMAT sample questions to get a sense for the exam. Here’s an official GMAT mini-quiz.

We’ve also created our own extra challenging GMAT sample questions with solutions. These practice questions can help you diagnose some of your issues so that you can improve your GMAT performance. Again, most of these examples are in the higher end of the difficulty range so if you struggle: DON’T PANIC! With organized practice you will gain the skills and confidence to solve this level of GMAT question.

These GMAT sample questions are unique in that they come with some very detailed explanations. Take your time to learn the methodology.There are lots of GMAT tips and tricks in these explanations that should help you on test day. For more GMAT practice questions and a whole bunch of strategies you can have a look at GMAT Question of the Day. Happy Studies and Good Luck!

GMAT SAMPLE QUESTIONS: PROBLEM SOLVING

GMAT Sample Question #1: Exponents

The expression above simplifies to a number that has how many digits which are divisible by 3?

A. 4,000,001

B. 24,000,001

C. 60,000,001

D. 60,000,010

E. 60,100,010

[spoiler]B.[/spoiler]

GMAT SAMPLE QUESTIONS: Exponents SOLUTION

This is a GMAT puzzle/exponents question. You will see GMAT questions which make you feel confused and rather uncomfortable but realize that all GMAT questions are based on simple rules. In general if you follow the rules you have a good chance of getting to the solution. Practice your fundamentals.

In this sample question we are dealing with exponent rules. Specifically what happens when a number is raised to a power? The exponents are multiplied. These numbers are enormous so it’s not practical to write everything out. We’re not looking for the final number but for the properties of the digits of the final number. In this case we know that the final number will start with a 6 and have 4,000,000 zeroes. Meaning – all of the digits will be divisible by three. Therefore 4,000,001 digits are divisible by 3.

GMAT Sample Question #2: Work/Rate

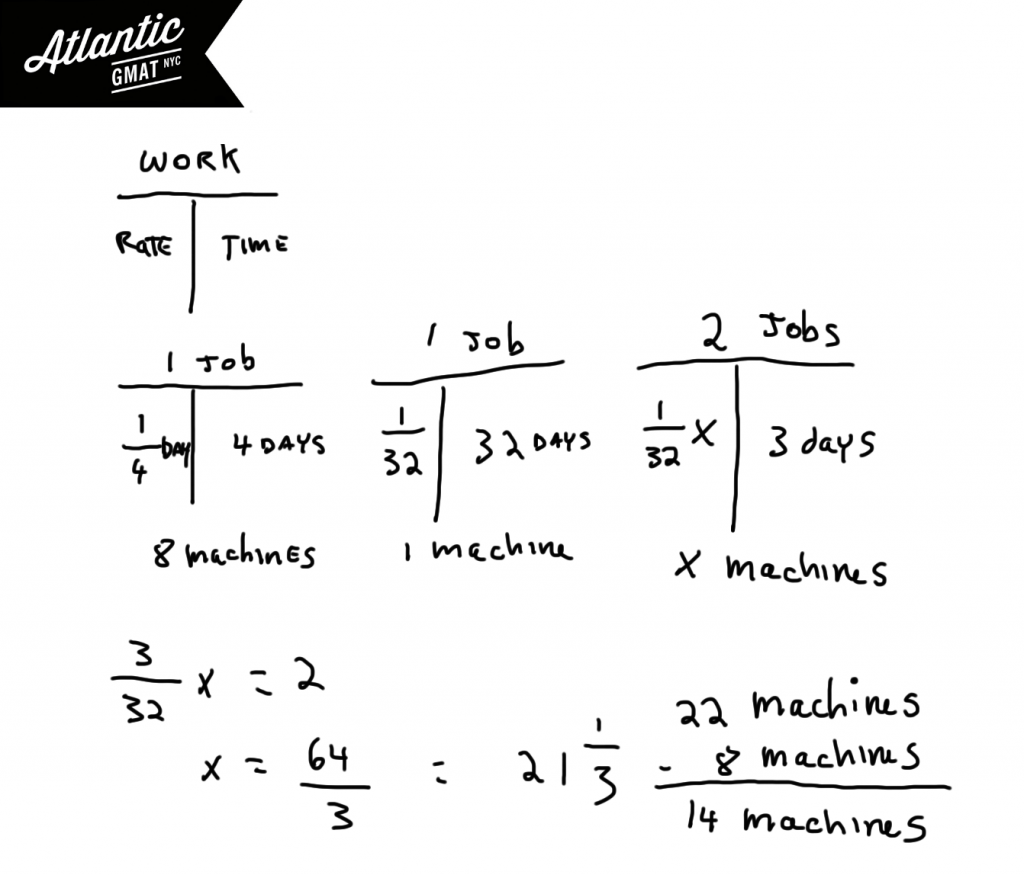
If 8 machines working together at identical rates can do a certain job in 96 hours then what is the minimum number of additional identical machines working at the same rate that must be added in order to complete two of these jobs within three days?

A. 10

B. 11

C. 12

D. 13

E. 14

[spoiler]E.[/spoiler]

GMAT SAMPLE QUESTIONS: WORK/RATE SOLUTION

Work and Rate questions are a staple of the test. They can be organized with T’s. The T allows you see all of the iterations of the Distance = Rate * Time formula. Yes – you can do these questions by setting up equations but most GMAT tutoring students do better using the T’s. Do you always have to use the T’s? No – but even just understanding how they work will make you a better GMAT test taker.

This GMAT sample question involves adding a certain number of machines in order to get a certain job done faster. With this question type it helps to find the rate for one machine. Then make a T with a variable representing the number of machines needed. This question adds a little twist: unit conversion. Just be careful with the arithmetic. Notice in the end that you will need 21 and 1/3 machines. You can’t have 1/3 of a machine so you will need 22 machines to get the job done within three days.

GMAT Sample Question #3: Percent Change/Ratio

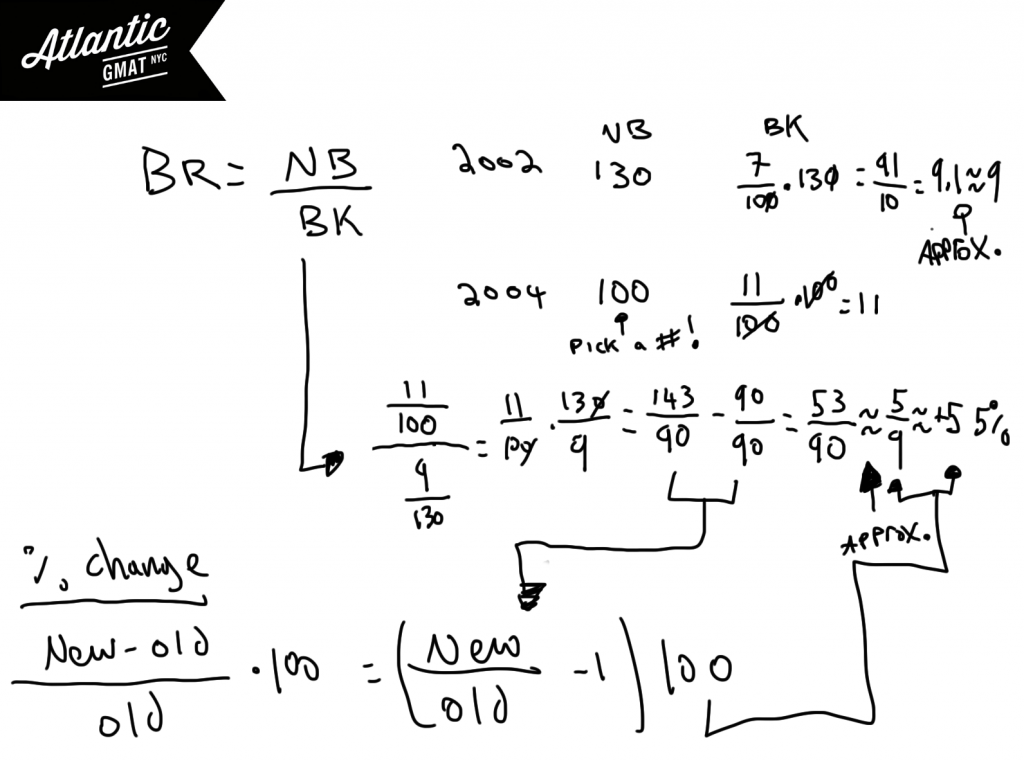
The bankruptcy ratio is defined as the ratio of new businesses started in a given year to the number of new businesses that declare bankruptcy in that same year. In 2002 7% of new businesses declared bankruptcy while in 2004 the corresponding figure was 11.3%. If there were 30% more new businesses started in 2002 than in 2004 what was the approximate percent change in the bankruptcy ratio from 2002 to 2004?

A. 22% Decrease

B. 45% Decrease

C. 22% Increase

D. 45% Increase

E. 57% Increase

[spoiler]E.[/spoiler]

GMAT SAMPLE QUESTIONS: RATIO/PERCENT CHANGE SOLUTION

This GMAT sample question is a classic word problem. Most GMAT tutoring students dislike word problems because this question type can be time consuming. There are three things that can help with GMAT word problems:

1. Take your time reading the question. Don’t worry about solving or doing calculations as you are reading. This is the time to think and process. To take in the big idea of the question.

2. After doing your careful read it’s time to define the actual question. This is an important but often forgotten step. Most people that I tutor (when we are just starting GMAT prep) jump right to calculating. This can work but you’ll set yourself up better and be prepared for the most challenging GMAT questions by defining what you are looking for. Not only will this guide you on the set-up but it will prevent you from making the mistake of choosing a “correct” value rather than the actual thing that the question was asking you to find.

3. Simplify when possible. Look for ways to make your arithmetic easier. This mostly comes down to reducing fractions before multiplying across. This way you’ll be dealing with the numbers in their simplest form. So: divide before you multiply. Also consider “massaging” values when doing so will create easy math. For instance, 7/99 is damn close to 7/100. The answer choices will dictate how far you can go with your approximations. The rule of thumb is keep your approximations in a smaller range than your answer choices. Realize though that multiple approximations can compound. Just keep in mind in which direction you have approximated. In the case above we know that our answer is a bit greater than 7%.

Practice your word problem approach so that it is second nature and easy to apply even under test day pressure.

 

 

GMAT Sample Question #4: Geometry

ABCDEF is a regular hexagon inscribed in square JKLM with vertices A and B on adjacent sides of the square and a center of O. If Q is the midpoint of AB and the area of square JKLM is √2 what is the area of triangular region OAQ?

A. (6^1/2)/32

B. (6^1/2)/16

C. (6^1/4)/16

D. (6^1/3)/16

E. (6^1/4)/8

[spoiler]B.[/spoiler]

GMAT SAMPLE QUESTIONS: GEOMETRY SOLUTION

These GMAT sample questions are challenging so again: don’t worry if you aren’t getting them on the first try. If you see questions like this one on your GMAT then you’re probably doing pretty well on the Quant section. Again, there is nothing super special happening here. There’s a hexagon inside of a square. You should know the formula for the sum of the interior angles of a polygon: (number of sides – 2)180. Divide that result by the number of angles in order to determine the measure of each angle. In this case each angle is 120 degrees. If you divide those angles in half by drawing lines from the center of the hexagon to the vertices you end up with 60 degree angles. You should notice that the hexagon is made up of 6 equilateral triangles. You don’t need that information for this question but it is worth keeping in your back pocket.

You also know that the area of the square is √2. Area = Side^2 so the sides of the square are 2^1/4 or the fourth root of 2. Notice that the side opposite the 90 degree angle is equal to half of the measure of the side of the square so (2^1/4)/2. Also notice that triangular region OAQ is a 30, 60, 90 triangle. Now just use those ratios to figure out the other sides and solve for the area. Again, take your time with the arithmetic (don’t forget to divide by 2 for the area of a triangle).

 

GMAT Sample Question #5: Combinations

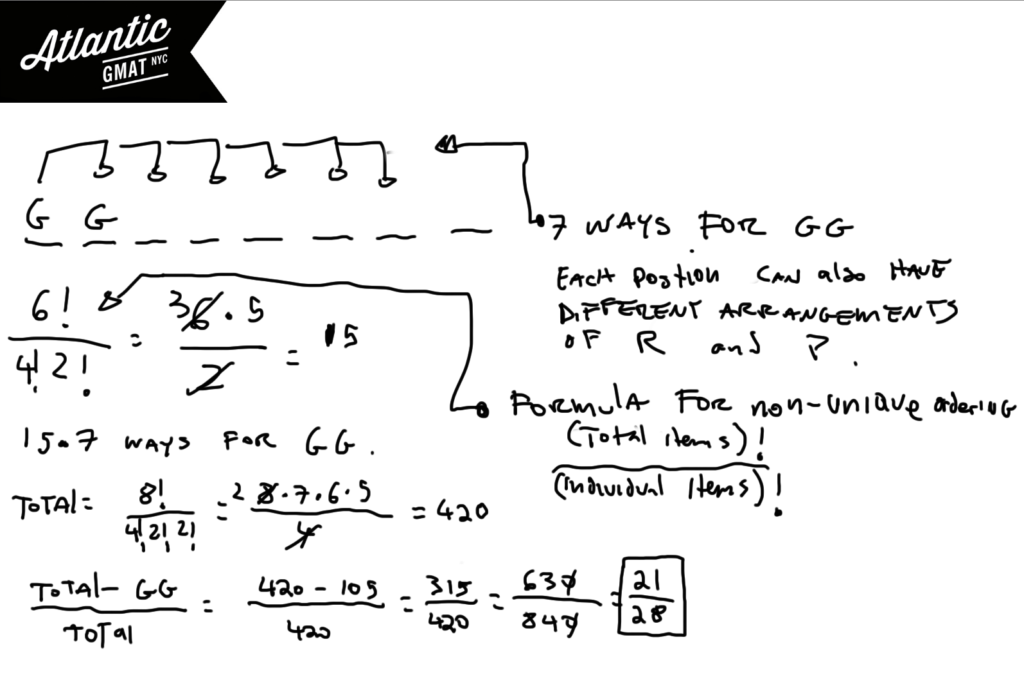
There are 4 red bottles, 2 green bottles, and 2 purple bottles. If the 8 bottles are arranged on a shelf what is the probability that no green bottle will be adjacent to another green bottle?

A. 3/5

B. 3/4

C. 11/14

D. 13/16

E. 13/15

[spoiler]B.[/spoiler]

GMAT SAMPLE QUESTIONS: COMBINATORICS SOLUTION

GMAT combinatorics questions can get your head spinning. If you can get through this one then you are on the right track (in general if you are doing well on these GMAT sample questions then your Quant is in excellent shape). This question is at least as tough as the toughest GMAT combinatorics questions that I’ve seen. When dealing with constraints always consider whether it might be easier to solve for the opposite of the constraint. Then you can subtract the opposite from the total and you will have solved for the constraint. For instance – if you want to know the probability of getting at least one tails in three flips of a coin you might consider solving for no tails and subtracting that from 1. This method can be a bit faster and easier to wrap your head around than a more straight ahead approach.

In this GMAT sample question consider finding all of the arrangements in which green will be next to green. Then you can take that number and subtract it from the total. Put that result over the total and you will have the answer.

 

Notice that as I worked through these GMAT sample questions that I had a plan for each one. I took a step by step approach to the solutions. This is something that comes up over an over again In GMAT private tutoring sessions: how to make an organized plan for a specific questions type. This organized approach to problem solving is even more important in the GMAT Data Sufficiency.

GMAT SAMPLE QUESTIONS: DATA SUFFICIENCY

GMAT Sample Question #6: Translation

If j and k are positive integers is (1.3k^2 – 5.2k^2)/.65 > 29?

(1)k – 3j > 4

(2) k = 5

[spoiler]A.[/spoiler]

GMAT SAMPLE QUESTIONS: TRANSLATION SOLUTION

If you see strange numbers on a GMAT question remind yourself that the GMAT will not ask you to do any intense arithmetic. Most likely there will be a way to simplify the expression. Look for ways to simplify. Most often you will be able to factor. Here we can factor out 1.3 and then divide by the .65. This will leave 2(k^2 – 4j^2) > 29? You can go one step farther by using the difference of squares: 2(k – 2j)(k + 2j) > 29? This is much simpler now.

(1) k – 3j > 4  Since k and j must both be positive integers this tells us that k – j must be greater than 4 (since k – 3j must be less than k-j). If that is true than k + j must greater than 4 (since k + j must be greater then k – j). So 2(k – j)(k + j) must be greater than 32. You can also say that k > 3j + 4. Since they are both positive integers, the minimum for j is 1 so the minimum for k is 7. So the minimum for 2(k – j)(k + j) is 56. Sufficient.

(2) k = 5. We could prove a yes and a no. If j = 1 then the value will be 32 (a yes). If j > k then the value will be negative (a no). Insufficient.

 

 

GMAT Sample Question #7: Perfect Fit

In 2002, Corporation J donated to charity 25 cents for each unit of product K sold and 49 cents for each unit of Product L sold. If Corporation J made no other donations that year, how many units of product L were sold?

(1) In 2002 Corporation J donated a total of $6.15 to charity.

(2) In 2002 there were twice the number of units of product K sold as there were of product L sold.

[spoiler]A.[/spoiler]

GMAT perfect fit questions can be quite challenging. These are a subtype of multiple equations questions. Here though you will be able to solve without having a 1:1 ratio of variables to equations because there is a perfect fit. One type of perfect fit (represented in this GMAT sample question) involves divisibility. There will a unique set of values for x and y. Why? Because x and y have to be integers. How do we know that? # of products sold must be an integer value as do people, marbles, cats, and houses (and many other things). You do not have to be told that these things must be counted in integers. That’s just the way it is. So if you have variables that must represent integers you should consider whether you have a perfect fit situation.

In this question we can start with the equation 25k + 49L = total donations.

Statement (1) This gives us the total, 615. Now start considering whether there’s only one combination of x and y that creates 615. Think of divisibility. 615 ends in 5 so the sum of 25k and 49l must end in 5. There are a limited number of ways that this can happen, 0 + 5 or 5 + 0. Make a chart to see if there is only one combination which yields 615. There is: 125 + 490. Sufficient.

Statement (2) This doesn’t provide a total and so there are limitless values for k and l.

GMAT Sample Question #8: Exponent/Threshold

Is 4^x > 1000?

(1) 5^(x-1) > 140

(2) x is an integer

[spoiler]C.[/spoiler]

GMAT SAMPLE QUESTIONS DATA SUFFICIENCY: EXPONENT/THRESHOLD SOLUTION

Organize your information so that it is easier to make inferences. So that it is easier to see the question. A good portion of DS is easy to solve but also easy to get wrong by overlooking a detail. In this GMAT sample question it will help to define the threshold. Where does 4^x cross the 1000 threshold? If we are thinking in integers the answer is 5. 4^5 is 1024. Of course x does not have to be an integer but it helps to define the threshold in terms of an integer value. So in this case we are wonder if x is greater than or equal to 5.

Statement (1) one tells us that x must be greater than 4. x could be just above 4 or x could be 100,000,000 because the sky is the limit. Therefore this statement is insufficient.

Statement (2) doesn’t tell us anything about the value of x. Insufficient.

Putting Statements (1) and (2) together we can conclude that x must be at least 5. Why? Because x cannot be a decimal. So if x must be greater than 4 and can’t a decimal than the next possible integer value is 5 which puts us above our threshold. Sufficient.

GMAT Sample Question #9: Multiple Equations

In 1993 the total revenues for Company L were 14,000,000 greater than they were in 1991. What was the percent change in profit for Company L from 1991 to 1993?

(1) Total costs for Company L remained unchanged from 1990 to1995.

(2) In 1991 Company L made 14,000,000 less in profit than in 1993.

[spoiler]E.[/spoiler]

GMAT SAMPLE QUESTIONS DATA SUFFICIENCY: MULTIPLE EQUATIONS SOLUTION

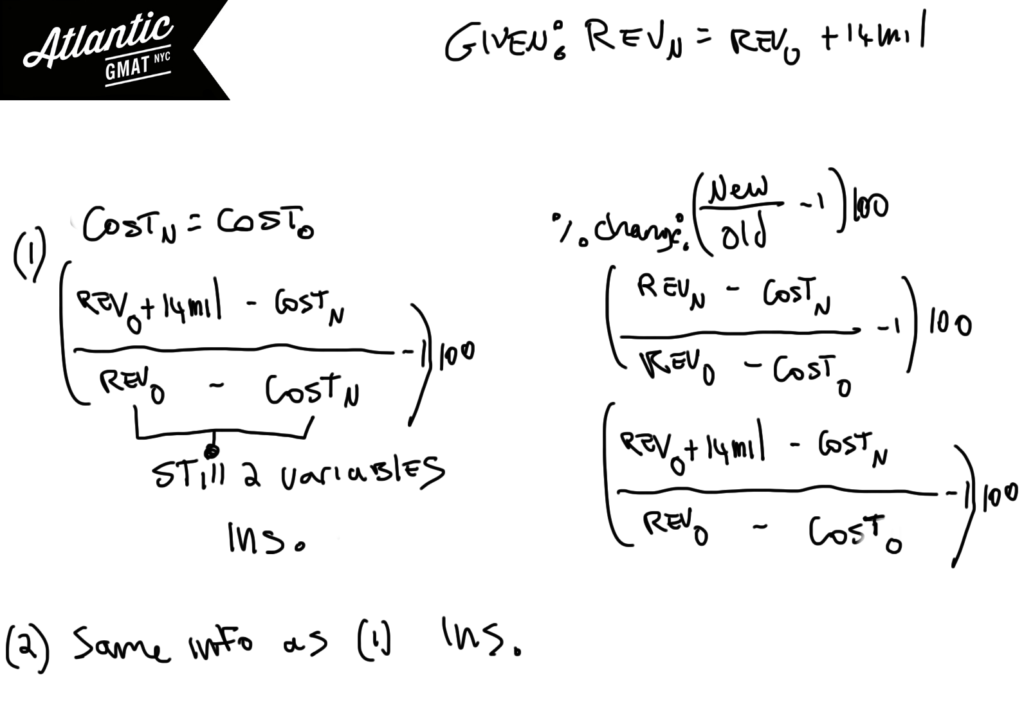
This is a classic GMAT multiple equations question. We are asked to figure out the percent change in profit from 1991 to 1993. Write out the percent change formula and you’ll notice that you have 4 variables: old/new revenue and old/new cost. We have one equation already, NEW(Rev – Cost) -14,000,000 = OLD(Rev – Cost). This indicates that unless there is something special happening that we will need 3 additional equations to solve.

Statement (1) Now we know that Cost New = Cost Old. Still we are left with two variables. Ins.

Statement (2) This is same information as the information from statement 1. This tells us that the costs were same. Ins.

Putting the statements together there is no new information. If you are finding these challenging don’t worry: these 10 GMAT sample questions are tough. If you can understand how to solve these questions then you will be in great shape for the real deal GMAT.

GMAT Sample Question #10: Number Properties

Is (x+j)(x+k)(x-m) a multiple of 3?

(1) j – k = m – j

(2) j, k, and m are consecutive integers.

[spoiler]B.[/spoiler]

You’ve made it to #10 of the GMAT sample questions! Congrats on getting here: This is some tough GMAT practice. There is a lot to learn here so certainly work these questions/explanations into your review. Let’s take a look at this last question:

Without knowing that the product of any three consecutive integers is divisible by 3 this sample question will be z challenge. Write out a few example so this makes sense to you. So if j, k, and m are consecutive integers then (x+j)(x+k)(x-m) will also be consecutive integers. Let’s also realize that x + 1 is the same as x + 4 in terms of divisibility by 3. Think of a few examples so that you get this straight: 1, 4, 7, 10… all numbers that when divided by 3 have a remainder of one. By the same token, x + 2 and x + 5 will have the same divisibility by 3. 2, 5, 8, 11, 14 are numbers that when divided by 3 have a remainder of 2. To sum it up, if you add three (or # divisible by 3) to a number, that number will maintain the same exact divisibility properties in terms of 3.

Statement (2) must be sufficient because that will make x + j, x+k, and x-m three “virtually” consecutive integers. The product of those integers must be a multiple of three. A little more on this idea: 1, 2, and 3 are consecutive integers. -2, 2, 3 are “virtually” consecutive in that you get a number from each remainder row in relation to 3. -2 is remainder 1, 2 is remainder 2, and 3 is remainder 0.

Statement (1) is insufficient because you can make all of the numbers 0 in which case the divisibility by three will be dependent on whether x is divisible by 3. This could be a yes or a no.

Were those GMAT practice questions tough? Well if they were that’s completely normal. Even my 700+ GMAT students might have a tough time with some of these GMAT problems. The important thing is to learn from these GMAT sample questions. Between the questions themselves and the explanations there is a wealth of knowledge.

Need More GMAT Sample Questions?

Here are a couple of other places where you can find quality GMAT sample questions:

1. GMAT Club also has a GMAT question of the day and many GMAT sample questions spread throughout the forum.

2. Of course there are also official GMAT sample questions. You can find more GMAT practice questions in the GMATprep software. Here you have two free resources: the GMAT prep exams which you should probably save for now and the question pack software which has an additional 75 free sample questions.

One last thing for the GMAT Beginner

If you are just starting out now is the perfect time to make a plan for your GMAT studying. Here is an article on creating a GMAT Study Schedule (and there is an 11 week schedule already made for you!), and here are some essential GMAT Study Skills. These two articles along with the GMAT sample questions and GMAT question of the day should help you create a solid foundation for your GMAT success.