Each year for 4 years, a farmer increased the number of trees in a certain orchard by 1/4 of the number of trees in the orchard of the preceding year. If all of the trees thrived and there were 6250 trees in the orchard at the end of 4 year period, how many trees were in the orchard at the beginning of the 4 year period? GMAT Explanation, Video Solution, and More Practice!
Each year for 4 years, a farmer increased the number of trees in a certain orchard by 1/4 of the number of trees in the orchard of the preceding year. If all of the trees thrived and there were 6250 trees in the orchard at the end of the 4 year period, how many trees were in the orchard at the beginning of the 4 year period?
A. 1250
B. 1563
C. 2250
D. 2560
E. 2752
Here’s another dense word problem from the GMAT Official Guide. This one tangles up tutoring students in the setup and then has a tiny bit of challenge in the follow through with some relatively big numbers. Let’s start by defining the question: How many trees were in the orchard at the beginning of the 4 year period? = How many trees did we start with?
OK, so we have the yearly growth rate (1/4) and the final tally after 4 periods of growth (6250) and with those two pieces of information we want to know how many trees we started with.
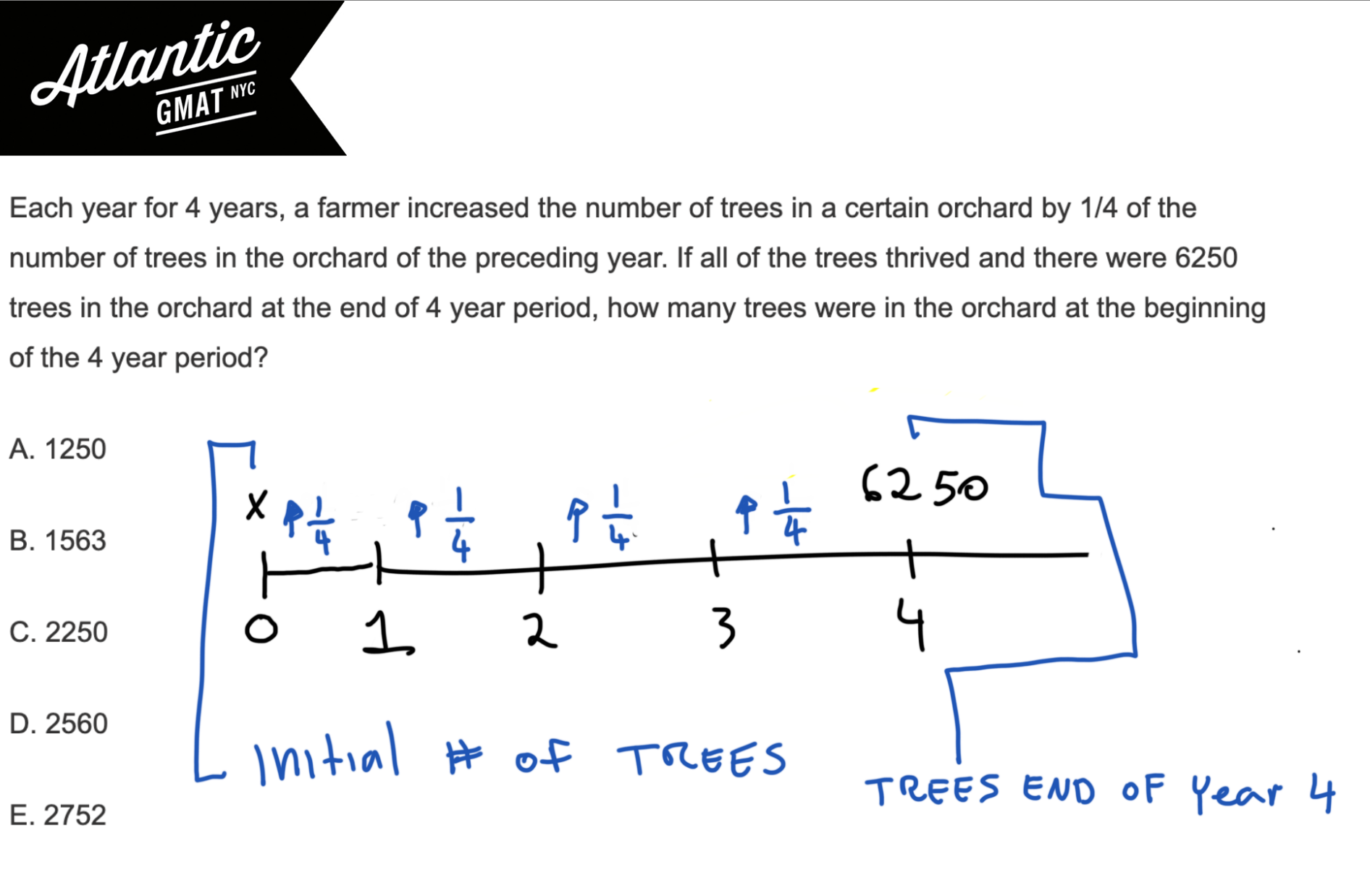
You want to have that structure in your mind before starting to do calculations! Also, for this question it could help to make a chart/timeline to illustrate the growth from end of year 1 to end of year 4. See example:
Let’s call the first year x. How do you grow x by 1/4? Multiply x by (1 + 1/4) or 5/4. After the first year we have 5/4*x trees. Then we multiply that by 5/4 to get year 2. Multiply year 2 by 5/4 to get year 3. Multiple year 3 by 5/4 to get year 4. In the end you’ll have something equivalent to this for end of year 4: 5/4*5/4*5/4*5/4*x or (5/4)^4*x.
We know there were 6250 trees in the orchard at the end of the 4 year period so (5/4)^4*x = 6250. Now we need to simplify that.
Multiply by the reciprocal to isolate x. 6250*(4/5)^4.
5^4 = 625 and 6250 = 625*10 so cancel the 625.
That leaves 10 * 4^4.
Because of the 10 we know the answer must end in 0. Because of the 4^4 we know the answer must be a multiple of 4. That leaves only 2560, D. Divisibility can be very helpful for eliminating answer choices.
That said, 4^4 isn’t hard to calculate. It’s 2^8. Since 2^10 is 1024, 2^9 is 512, 2^8 is 256. I’d memorize 2^10 so you can work your way down to those higher powers of 2. It’s also good to know because it’s very close to 10^3 and powers of 10 come up a lot.
Here’s the full solution with diagram:
Video Solution: Each year for 4 years, a farmer increased the number of trees in a certain orchard by 1/4 of the number of trees in the orchard of the preceding year. If all of the trees thrived and there were 6250 trees in the orchard at the end of the 4 year period, how many trees were in the orchard at the beginning of the 4 year period?
Additional GMAT Problem Solving Practice Questions
Here’s a very similar one from the GMAT Prep Official Practice Tests 1 and 2: When a certain tree was first planted, it was 4 feet tall