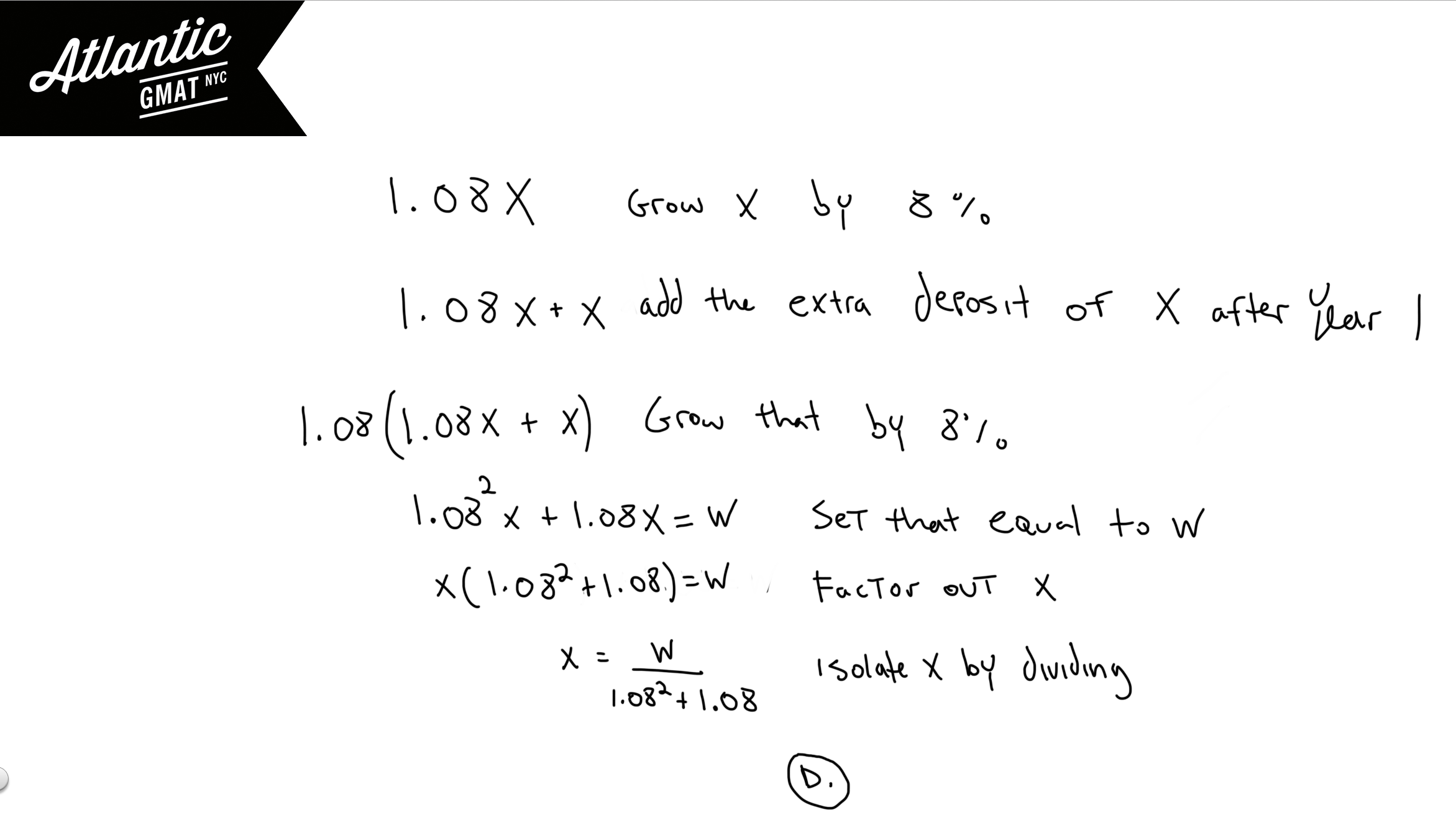Alex deposited x dollars into a new account that earned 8 percent annual interest, compounded annually. One year later Alex deposited an additional x dollars into the account. If there were no other transactions and if the account contained w dollars at the end of two years, which of the following expresses x in terms of w?

Alex deposited x dollars into a new account that earned 8 percent annual interest, compounded annually. One year later Alex deposited an additional x dollars into the account. If there were no other transactions and if the account contained w dollars at the end of two years, which of the following expresses x in terms of w?

A. w/(1+1.08)

B. w/(1.08+1.16)

C. w/(1.16+1.24)

D. w/(1.08+1.08^2)

E. w/(1.08^2+1.08^2)

We need to get x in terms of w. So, what does that mean? This is important because it comes up often on the GMAT. x in term of w or anything in terms of anything else means: x = w (multiplied by, divided by, added to, subtracted from something). So x on one side by itself. w on the other side with some sort of operation which, of course because it’s an equation, makes w equal to x. Make sure you understand that! OK, on with Alex and his dollars. Video solution and diagram below!

Take your time reading and understanding the question. When this one comes up in tutoring sessions the problem is often that the student has misread something. In this case Alex’s x dollars are growing at 8 percent annual interest. How do you grow something at 8%? Well, add 1 to the decimal equivalent of the percent and multiply that by the money. So, 8 percent = .08. Add 1, 1.08. Multiply by x = 1.08x. So that’s after our first year, we have 1.08x. Then we an additional x dollars. OK. so 1.08x + x is our total after year one. And then in the second year that amount grew by an additional 8 percent so multiply the whole expression by 1.08.

1.08(1.08x + x)

1.08^2x +1.08x = w

To get x in terms of w we need to get x by itself. So factor it out.

x(1.08^2 + 1.08) = w

Now just divide by (1.08^2 + 1.08)

x = w/(1.08^2 + 1.08)

D.

Additional related GMAT Practice

Here is another word problem with some algebra/arithmetic follow through from the GMAT prep tests: When a certain tree was first planted