A rectangular photograph is surrounded by a border that is 1 inch wide on each side. The total area of the photograph and the border is M square inches. If the border had been 2 inches wide on each side, the total area would have been (M + 52) square inches. What is the perimeter of the photograph, in inches? GMAT Explanation + Additional Examples!
A rectangular photograph is surrounded by a border that is 1 inch wide on each side. The total area of the photograph and the border is M square inches. If the border had been 2 inches wide on each side, the total area would have been (M + 52) square inches. What is the perimeter of the photograph, in inches?
A. 34
B. 36
C. 38
D. 40
E. 42
Define the question: What is the perimeter of the photograph, in inches?
This is simple enough, but let’s pick out exactly what we’re looking for here. Since this is a pretty visual question, let’s draw out a diagram.
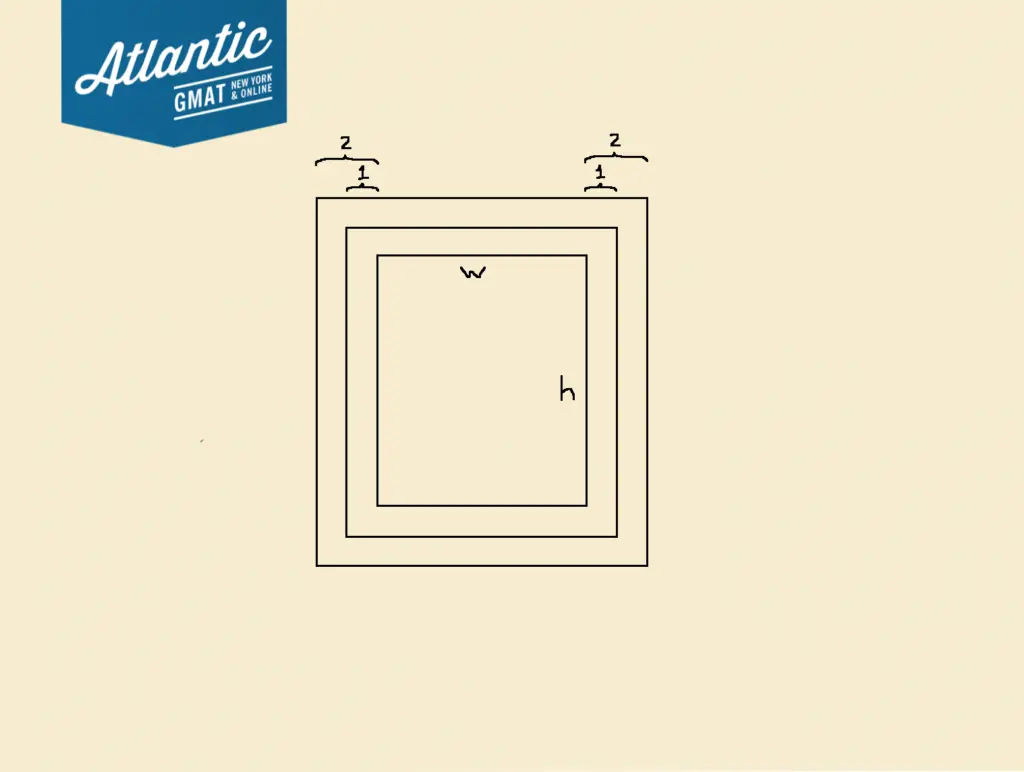
Here, we have the photograph with two different border widths, labeled with their sizes. I also gave variables w for the width of the photograph and h for the height.
The question gives us areas for the photograph with borders, but we are looking for the perimeter of the photograph, not the area. The perimeter of the photograph is 2w + 2h, so we need to find the values of w and h.
Organize the information:
Here, we have two different areas given to us. With a 1 inch border, the total area is M. With a 2 inch border, the total area is M + 52.
Think carefully about what a border means. This adds extra length to every side of the photograph. Let’s write out a formula for the area of the photograph and 1 inch border with this in mind.
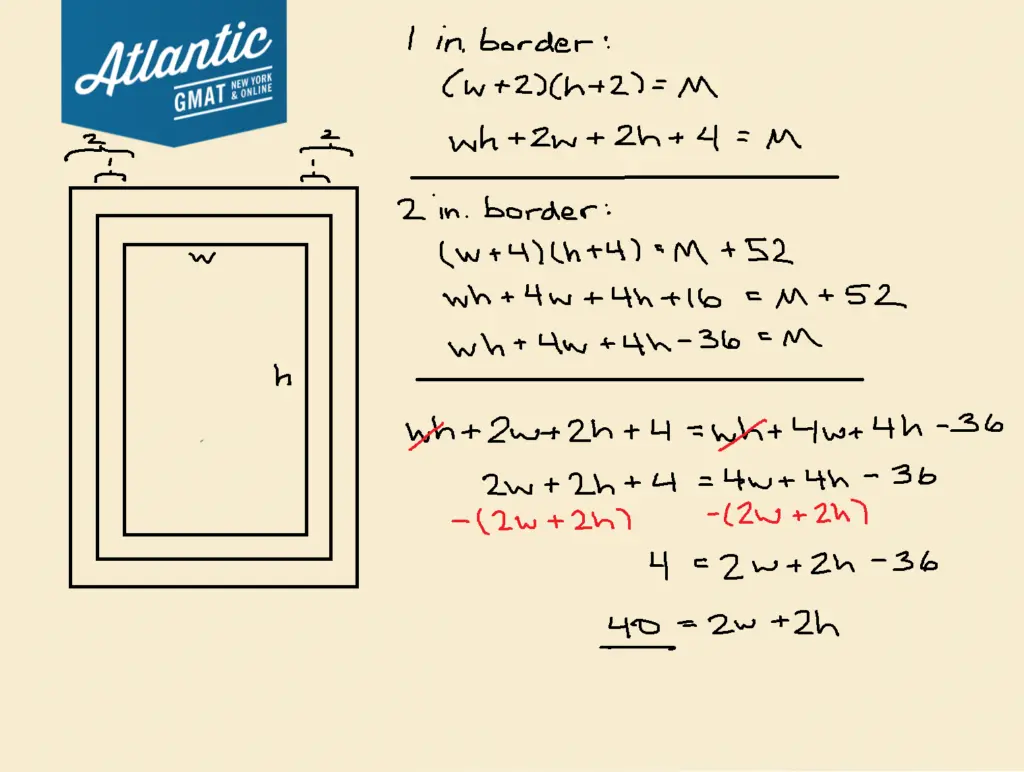
The area of a rectangle is given by width times height. For the photograph and 1 inch border, the width is w plus 1 inch on the left AND 1 inch on the right. So this width will be w + 2. We do the same for the height. This will be h plus 1 inch on the top and one inch on the bottom, so h + 2. Our equation for area is:
(w + 2)(h + 2) = M
Multiplying this out, we get:
wh + 2w + 2h + 4 = M
Now, we do the same for the 2 inch border, remembering we add 2 to each side now. In this case, we have a width of w + 4, and a height of h + 4. Therefore, this equation for area is:
(w + 4)(h + 4) = M + 52
Multiplying this out and solving for M, we get:
wh + 4w + 4h + 16 = M + 52
wh + 4w + 4h – 36 = M
Time for some algebra:
Now, we have both area equations equal to M. Let’s set them equal to each other:
wh + 2w + 2h + 4 = wh + 4w + 4h – 36
Let’s subtract wh from both sides:
2w + 2h + 4 = 4w + 4h – 36
Now subtract 2w + 2h from both sides:
4 = 2w + 2h – 36
And finally add 36 to both sides:
40 = 2w + 2h
Remember, we were looking for the perimeter here, which is 2w + 2h. Well, that’s exactly what we got here! So it looks like our answer is 40.
Answer: D
Here is that all worked out: