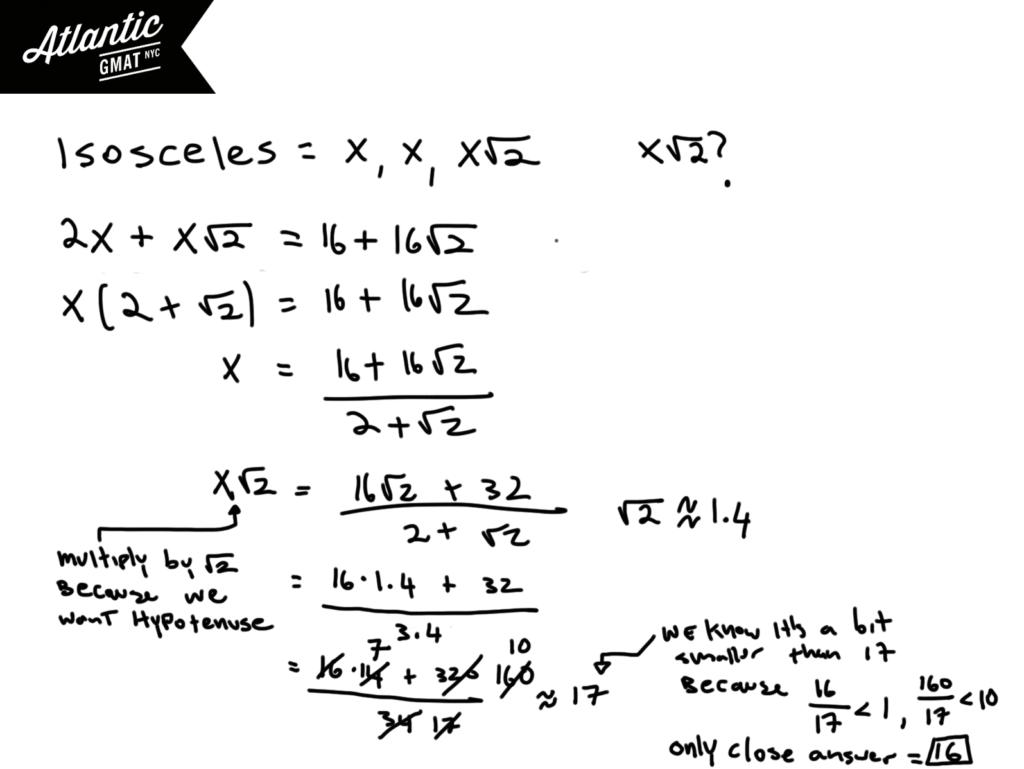(A) 8
(B) 16
(C) 4√2
(D) 8√2
(E) 16√2
A lot of people get this GMAT geometry question from the GMAT prep software wrong. It’s true that the algebra gets a little tricky but conceptually there’s not much going on. We just need some basic triangle rules and vocabulary (perimeter, isosceles, right triangle…) And, to add, there are three ways to solve this thing. You can tackle the algebra, plug in answer choices, or you can even estimate. We’re going to take a look at each solution below.
Let’s start with the algebraic solution
Table of Contents
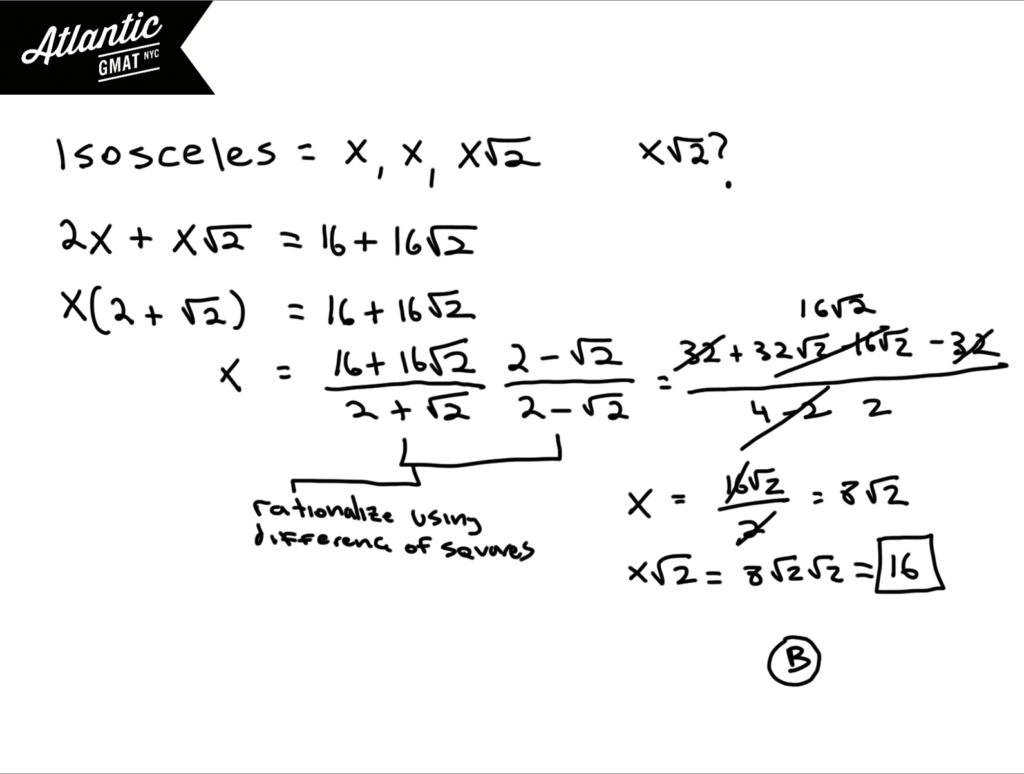
You need to know that the sides of an isosceles right triangle are always in the ratio x, x, x√2. No excuses for not knowing GMAT basics. You have to be fluent with the fundamentals so that you can focus on what the test is really about: critical thinking.
The perimeter of this isosceles right triangle then is 2x + x√2. And. according to the given information, that perimeter equals 16 + 16√2. About half of people stop here and stay: Bingo! The hypotenuse of the triangle must be 16√2!!! Nope.
That’s some fuzzy logic. Let’s keep simplifying by trying to isolate the variable. You can do that by factoring out the x. Do you know how to get rid of radicals in the denominator (rationalizing)? Well, that’s another basic that you’ll need to conquer the GMAT quant. Keep in mind that we’re solving for x√2 (the hypotenuse). See the diagram below for the worked out solution.
You can also use the answer choices
I’d still do a bit of simplifying but then you can plug in the answers and see if the equation stays balanced (what is on the left equals what is on the right). Again, keep in mind that the answers are the hypotenuse, x√2, not x. So in order to plug them in for x we need to divide them by √2. Sounds more complicated than it is. Plugging in answers ends up being even easier than the algebra.
Last but not least you can estimate
Estimation is a very helpful tool for getting through some GMAT questions. My advice is:
- Keep your approximation/estimation in line with how far apart the answer choices are. In this case our approximations are within 10% and the closest answers are about 30% apart giving us some breathing room.
- Use estimation/approximation as a useful tool deployed when appropriate not as a crutch for when you’re in panic mode.
Here we just have to call √2 1.4. After that the arithmetic is basic. You can multiply everything by 10 to get rid of the decimals and then simplify. 16/17 is so close to 1 that we can just call it 1. 160/17 is very close to 10. With that we get 17. But we know that we’re a tiny bit less than 17. The only answer that’s remotely close is 16. 16√2 is almost 24. 8√2 is little less than 12. Those are way too far off to be considered.
Here’s the video solution for: The perimeter of a certain isosceles right triangle is 16 + 16√2. What is the length of the hypotenuse of the triangle?
More Challenging GMAT Geometry Examples Involving Isosceles right triangles
This is one of the toughest GMAT questions ever. In a lot of ways the solution is very basic but most people don’t get there or even close. This one is a notch tougher than the one above and I really don’t expect most people to get it correct. I’d be 50/50 on this if I saw it on an exam. Still, it’s a great learning question as it can reveal that the quant part of the GMAT is simple. There’s no fancy math here. It’s all about understanding the given information and the question and getting it all organized: In the figure above, each side of square ABCD has length 1, the length of line segment CE is 1, and the length of line segment BE is equal to the length of line segment DE. What is the area of the triangular region BCE?
This one doesn’t involve right isosceles triangles but I think it’s very similar because the geometry aspect is basic but the follow through and algebra gets a little tricky: A small, rectangular park has a perimeter of 560 feet and a diagonal measurement of 200 feet. What is its area, in square feet?
Here’s another right isosceles triangle question from the GMAT Official Guide that’s very similar in difficulty to the above: In the figure above, is the area of triangular region ABC equal to the area of triangular region DBA?
Here’s one from the GMAT Prep Tests 1 and 2 that has a similar feel. The focus is on the algebra/setup not the geometry:
And a similar right isosceles triangle question from GMAT question of the day along with a GMAT question of the day geometry puzzle.
Happy studies!