GMAT Question of the Day – Problem Solving – Rate
A driver completed the first half of a trip at an average speed of 30 miles per hour. What speed must the driver average for the second half of the trip in order to average a speed of 36 miles per hour for the entire journey (assuming that the driver did not make any stops during the trip)?
A. 42
B. 45
C. 48
D. 50
E. 52
[spoiler]B.[/spoiler]
GMAT Question of the Day Solution
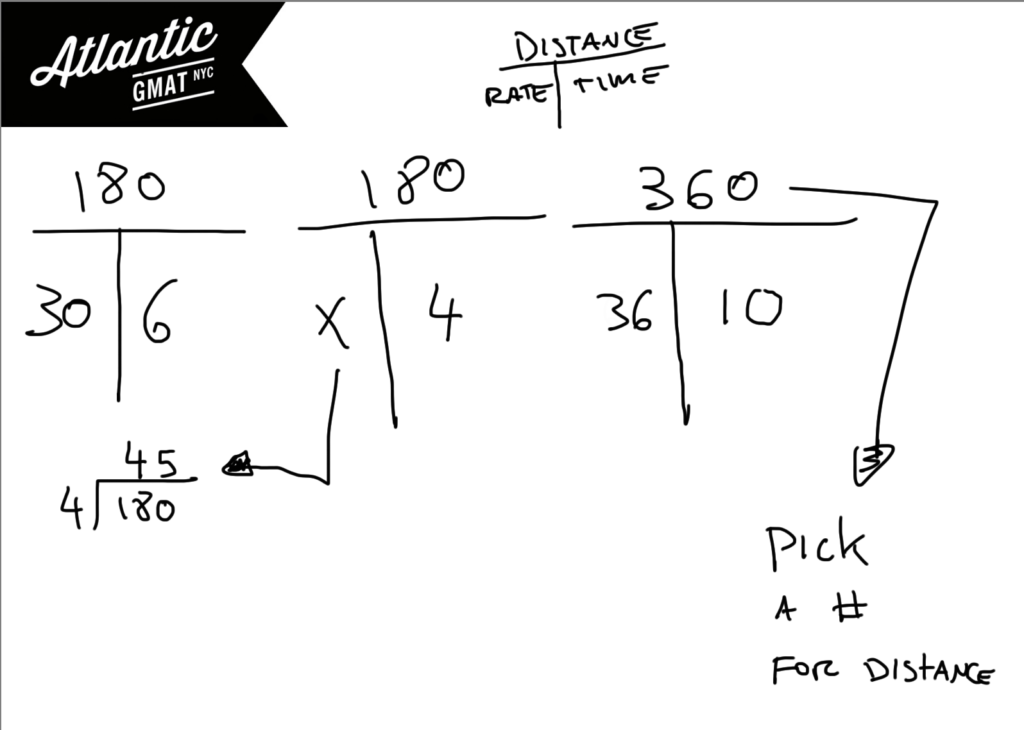
This is a classic GMAT rate question: average speed for a two part journey. Let’s remember that with average rate you can’t simply take the average of the rates because doing so assumes that you spent an equal amount of time driving at each rate. Usually that’s not the case so you need to add a “weight” to each of the rates before combining them. The “weight” is how much time you spent driving at that rate.
The general strategy for GMAT weighted average/rate questions is to make a T for each part of the journey. In this case you would have the two pieces and the total. The time boxes for each of the pieces sum to the total time. The distance boxes sum to the total distance. Divide the total distance by the total time to solve for the “total” rate.
In this question you are given the total rate and need to work backwards in order to solve the rate for the second half of the journey. The procedure is the same. Work with the time and distance in order to calculate the rate. We are not given a number for the total distance but we can certainly pick a number so that the question comes more into focus. Pick a number that works nicely with the given information. In this case a multiple of 180 will work well with 30 and 36. Here’s an Official GMAT question on which we also use the T method: A boat traveled upstream a distance of 90 miles at an average speed of (v-3) miles per hour and then traveled the same distance downstream at an average speed of (v+3) miles per hour
Here are more GMAT average rate practice questions:
Distance, Work and Rate – Average Rate 1
Distance, Work and Rate – Average Rate 2
For more GMAT distance, work, and rate practice visit GMAT Question of the Day.