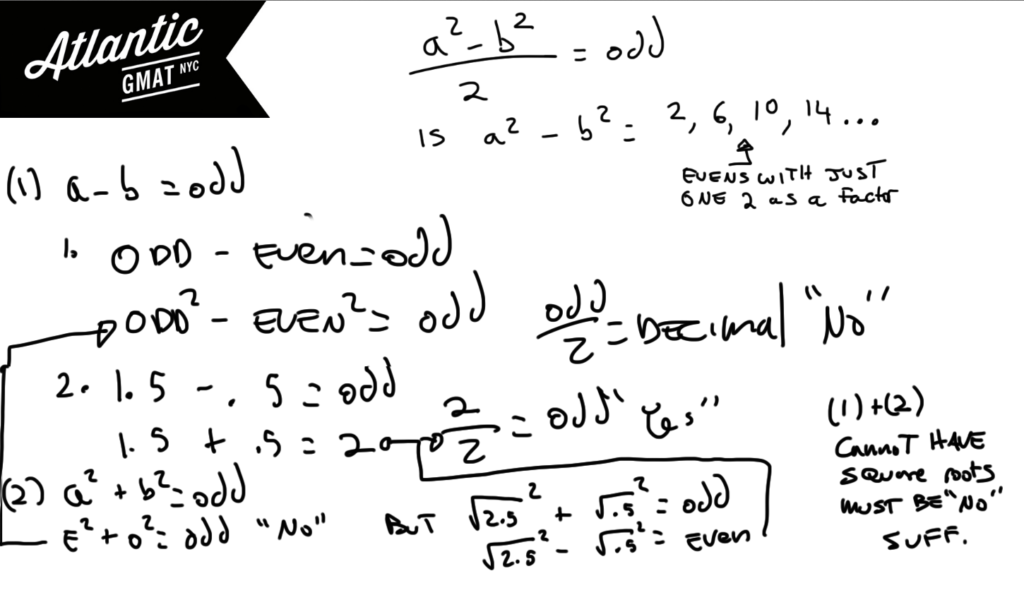GMAT Question of the Day – Data Sufficiency – Number Properties/Odds and Evens
Is /2 an odd integer?
(1) a-b is odd
(2) is odd
[spoiler]C.[/spoiler]
GMAT Question of the Day Solution
For this question of the day it’s important to remember one thing: a and b don’t have to be integers. With GMAT tutoring students I often see this idea of integer v. non-integer overlooked, especially in the Data Sufficiency. Remember special numbers: 1, 0, Negative, Positive, Integer, Decimal.
Let’s simplify this question a bit more. What is it really asking? What type of number when divided by two becomes an odd integer? Certainly not an odd number and certainly not a decimal. So what’s left? Even. But not any even. For instance, 4/2 is even. But 6/2 is odd. So we’re wondering whether the numerator (a^2 – b^2) is an even number with only one 2.
If a and b are integers then statement (1) tells us that the expression will yield a decimal. So the answer would be No. However, a and b could be decimals. (1.5+.5)(1.5-5) = 2. 2/2 = Odd. This is a Yes. Yes/No means insufficient. With statement (2) you also have two options. Both number could be odd integers in which case the answer is No. However, a could be √2.5 and b could be √.5 so that a^2 – b^2 yields an even number with only one 2. This would be a Yes. So statement (2) is insufficient. Putting them both together the square roots are not possible because they will not work with statement (1). So the answer is a definitive No.