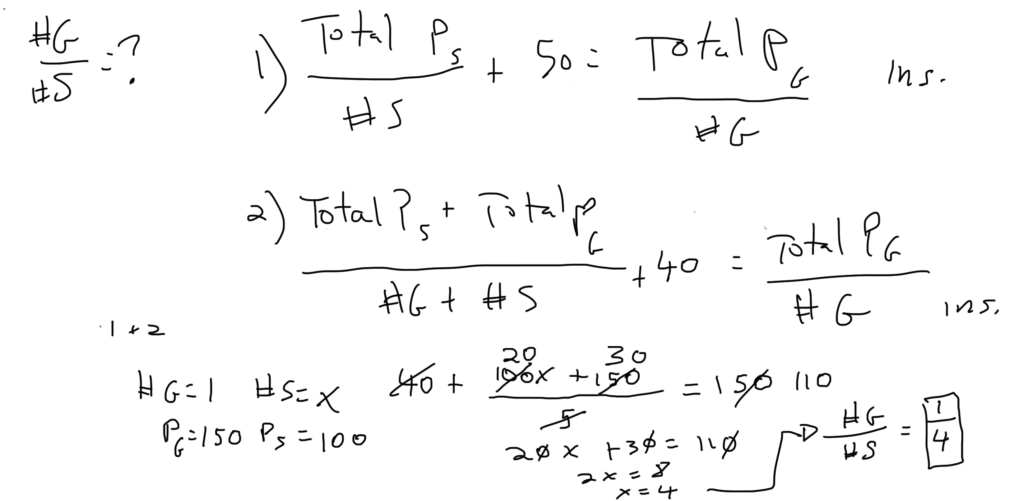GMAT Question of the Day – Data Sufficiency – Weighted Average/Ratios
Each Doctor at a certain medical practice is either a specialist or a generalist. What is the ratio of generalists to specialists?
1) The average (arithmetic mean) number of procedures performed per year by specialists is 50 less than the average (arithmetic mean) number of procedures performed per year by generalists.
2) The average (arithmetic mean) number of procedures performed by generalists is 40 more than the average (arithmetic mean) number of procedures performed by all of the doctors at the practice.
[spoiler]C.[/spoiler]
GMAT Question of the Day Solution:
The question is asking about ratios/proportions so think about picking numbers. It should be clear that each piece of information on it’s own is insufficient. There are too many moving parts. Try a few different sets of numbers to prove this to yourself. Putting things together the results are locked into a ratio of 1:4. Again, pick numbers for this. You know that there must be more specialists than generalists so assume that there’s only one generalist and that there are x specialists. Also from statement 1 you know that the average for generalists is 50 more than the average for specialists. So you can pick numbers to represent this. I chose 150 for the generalists and 100 for the specialists. Set up the equation and solve for x.